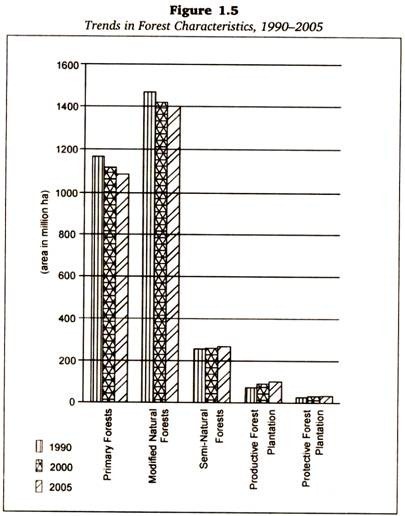
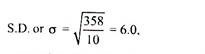Volumetric oxygen transfer coefficient (KLa) serves as a determinant of aeration efficiency of a bioreactor.
Maintenance of uniform KLa throughout the liquid is most important in aerobic submerged fermentation.
In fact KLa is influenced by several factors as described in the following sections:
1. Broth viscosity:
A relation between apparent viscosity (ηapp) and KLa for penicillin fermentation broth was provided by Deindoerfer and West (I960). Other available information’s also described the influence of broth consistency on oxygen absorption (Jarai et al, 1969 and Taguchi, 1971). For same volume and similar geometry of the vessel change in rheological property of the broth changes KLa value during fermentation.
Fermentation broths of penicillin, nystatin, cycloserine and some other antibiotics confer this property. They are highly non-Newtonian and contain mold myceleum in pellet or dispersed forms in the broth. A relation of change of KLa with broth consistency index (K) along with other parameters like surface tension, flow behavior index (n) and culture age of cycloserine fermentation has been provided by Jarai et al. (1969). A continuous decrease of KLa with fermentation age was observed. The increasing value of K and slowly decreasing value of n might be the cause of such a decrease of KLa.
A logarithmic relation between decrease of KLa and ηapp was shown in penicillin broth (Deindoerfer and West, 1960). Besides ηapp other engineering parameters like power input per unit volume (PA/), impeller spacing to its diameter (S/D ;), linear air velocity (Vs), impeller speed (N) also exercise their effects on oxygen absorption capacity of the system. Mathematically, therefore,
Where f represents a function of the variables indicated in the bracket and α, β, γ, δ and Ө are exponents. Maximum oxygen transfer rate (OTRmax) in the broth can be computed from
OTRmax = KLam(C*-CL) (5.45)
Where KLam is the maximum value of KLa under optimum operating conditions of the engineering parameters. Maximum oxygen demand over OTRmax can then be assessed easily. Under steady state oxygen uptake rate (OUR) would be such that
OUR < OTRmax (5.46)
Where OUR = r Cx (5.47)
r being specific oxygen uptake rate, m mole O2 consumed g-1 hr-1 and Cx is cell concentration gl-1. Change in broth rheology during fermentation can affect OTR as well as OUR by increasing resistances to oxygen transfer pathways and rendering poor flow condition in the fermenter.
2. Power expenditure:
With the variation of power expenditure for aeration and agitation in fermentation oxygen transfer rates vary appreciably. Quantitative relationship between power expenditure in aeration and agitation in fermentation oxygen transfer rates vary appreciably. Quantitative relationship between power expenditure in aeration and agitation has been developed by many workers (Mitchell & Miller, 1962, Kanzaki et al, 1968).
Analysis of the data provided by Taguchi (1968) as shown in Table 5.4 indicates the significance of power expenditure on aeration. It shows that the agitational power (KWH/Kg broth) is increased by about two times when fermenter volume increases ten folds while air compression energy increased by about three times. At this condition total energy expenditure per kilogram of oxygen transferred is just a little over double.
Data of Kanzaki et al, (1968) obtained with Na2SO3 solution in 4200 I fermenter (Table 5.5) further show that for the same liquid volume a threefold increase in agitation power increases total energy requirement by two fold when OTR increased from 20 to 100 m mole T1 hr-1. The corresponding increase in energy requirement for air compression is five fold. Bylinkina et al., (1972) observed in oxytetracyclin fermentation that OUR changes depending on the energy expended in impeller rotation with reference to various periods of its production.
Table 5.4: Oxygen transfer rate (OTR) as a function of power expenditure in non-Newtonian broth (calculated from the data of Taguchi et al (1968))
3. Vessel geometry and liquid depth:
Geometric parameters of the vessel have a marked effect on oxygen absorption. Influence of the ratio of impeller diameter to fermenter diameter (Di/Dt) on oxygen absorption has been reported by some workers. The flow component of power consumption is greater and turbulence component is less with larger Di/Dt ratio.
Larger impeller with higher flow component would effect a more uniform distribution of oxygen transfer throughout the fermenter. The smaller impeller causes a high local turbulence and increased OTR in viscous fermentation fluids. However, with sulfite and non-viscous fluids all impeller diameters produce almost same oxygen absorption rate. Different conditions showing oxygen transfer coefficient as function of fermenter geometric parameters has been presented in Table 5.6.
Influence of liquid depth and fermenter geometry on oxygen absorption can be visualized from the report of Lister and Boon (1973). In deep tank agitation vessel (like batch air lift fermenter) the conventional oxygen absorption equation (5.7) requires modification as C*, which is usually assumed constant, will actually depend on liquid depth since partial pressure of oxygen in bubbles and OTR from the same depends on their position under hydrostatic head.
The composition of the air bubble flowing throughout the liquid will vary from bottom to the top of the tank and with time during the experiment. The modified oxygen absorption equation will then be given by
Here Csi is the saturation concentration of oxygen when water is in equilibrium with inflowing air in which the proportion of oxygen is Xi, X0 is the proportion of oxygen in out flow air from the vessel.
Downing (1960) observed in a furrow bottomed tank that KLa and oxygenation efficiency decreased with increase in liquid depth. In a square section tank fitted with dome diffuser Lister and Boon (1973) measured DO concentration at different liquid depth and could not notice appreciable change in KLa and oxygenation efficiency at different depths.
It was, therefore, contradictory to Downing’s report. However, when they conducted the experiments with flat bottomed tank modified to a furrow similar to that used by Downing they could observe comparable results. It was concluded that the differences in the results obtained between furrow and square bottomed tanks was due to difference in their geometry.
The vessel shape determines the hydraulic mixing pattern in the tank under different conditions of aeration. Improved mixing in furrow vessel resulted higher relative velocities of air bubbles and the liquid ultimating increased oxygen transfer coefficient. So considerations of fermenter vessel geometry and liquid depth in it are important in oxygen transfer studies.
It is clear from the above discussions in aerated well mixed STBR one may conceive the existence of distributed tiny and large air bubbles throughout the liquid in a given bioreactor/ fermenter vessel geometry and liquid depth. So, in computation/ measurement of overall volumetric oxygen mass transfer coefficient (VOMC, KLa) there will be contributions from both tiny and large air bubbles in the system.
Tiny bubbles fraction receives a supply of oxygen continuously through the fraction of sparged air flowing (FQG) through the liquid. Considering the whole system of tiny bubbles one may write an oxygen balance equation covering this fraction as below (5.50).
In this equation P0 is the atmospheric pressure, f is the mole fraction of oxygen in the inlet, f is the mole fraction of oxygen in the tiny air bubble fraction, R is the universal gas constant, T is the experimental temperature in absolute scale, (KLa)t is the VOMC due to tiny bubbles, C2 is the solubility of O2 corresponding to the tiny bubble fraction and CL is the concentration of dissolved oxygen in the feed of the bioreactor and V is the liquid volume. In the above equation the first and second terms on the left hand side represent the rates at which oxygen flows in and out of the tiny bubble fraction, respectively. Third term in this equation represents the rate of oxygen transfer to the liquid through this fraction. The solubility of O, corresponding to its partial pressure in the tiny bubble fraction is computable from C, = P°Y/H, here H* being the Henry’s constant.
Further, also following assumption that a large bubble fraction flowing through the liquid in a plug flow manner with oxygen partial pressure (P.P.) comparable to that of the inlet air, the solubility of oxygen corresponding to its partial pressure in the large bubble fraction is given by
From measurements, low value of ND will indicate that the tiny bubble fraction is actively transferring oxygen. For extreme case when ND –> O equation 5.42 gives C*2 = C1 indicating that solubility’s and oxygen partial pressure of the large and tiny bubble fractions are similar.
In contrast, a high value of ND indicates greater mean residence time of the tiny bubbles in relation to the characteristic time for oxygen transfer, which enables tiny bubbles to equilibrate with the liquid. For the case where ND >>1 equation 5.54 simplifies to C* = CL. It is now possible to estimate the ratio of the rates of oxygen transfer between large bubbles (y1) and tiny bubbles (yt) that can be expressed by
This implies that in a continuously stirred tank aerobic/oxic bioreactor half of the oxygen mass transfer might be considered to take place through tiny bubbles. Also, this analysis reveals that tiny bubbles in viscous liquid cannot be assumed to equilibrate with the liquid phase.
4. Antifoam and impurities:
Several reports concerning the effect of antifoam agents on oxygen transfer are available (Evans and Hall, 1971; Mimura et al., 1973; Bell and Gallo, 1971). Since fermentation is usually conducted at constant temperature and pressure so thermodynamically antifoam agents make the foam unstable causing ∆G < va ∆A (where AG is the free energy change, va is the surface tension and ∆A is the change in area).
At this condition it destroys the surface elasticity and viscosity of the air bubble and spreads quickly over the bubble lamellae. On the basis of the above reports it appears that as the antifoam agents spread over the bubble depending on their concentration they can influence on KLa in different ways as classified below.
Decreasing Effect:
It might:
(i) Be due to formation of larger bubbles with smaller surface to volume ratio,
(ii) Decrease in residence time of the bubbles and hold up volume when foaming is restricted and
(iii) Cause additional gas liquid interfacial resistance resulting from the barrier imposed by the agent forming a film around the bubbles.
Thus in bubble dispersion systems KLa decrease by antifoam can be due to the decrease of KL or a or both.
Increasing Effect:
It is due to the release of bubbles from adsorbed cells there by making it unstable and rendering larger interfacial area between air and liquid thereby increasing KLa. Bell and Gallo (1971) showed (Table 5.7) that minute amount of adventuties surface active impurities improved oxygen transfer in the liquid. The action of these contaminants was greater in the alkaline range.
Mimura et al. (1973) observed in hydrocarbon fermentation by yeast cells that air bubbles which are completely covered with yeast cells become very stable. Addition of silicone oil, however, makes such bubbles unstable and release yeast cells from their surface. It causes higher oxygen consumption rate by the cells and aids in higher oxygen absorption in the culture liquid. KLa value also becomes three times higher than KLa measured without the antifoam in the liquid.
Antifoams which cause bubble coalescence and short-end residence time reduce oxygen transfer rate by effecting mainly on gas-liquid interfacial resistance. Those lowering surface tension increase oxygen transfer rate which might be due to decreased bubble size rather than any direct-interfacial film effect.
5. CO2 accumulation:
In cases of secondary metabolism of microorganisms CO2 plays a role, both in dissolved and in gaseous phase, on oxygen transfer in the liquid. Our present knowledge regarding the extent of this factor as a controlling one is rather limited. Inhibitory effect of CO2 accumulation on fermentations like glutamic acid (Hirose et al, 1973 & Okada and Sonoda, 1965), inosine (Shibai et al., 1973) and in some other microbial fermentations are reported.
Okada demonstrated that removal of C02 from the environment by increasing air flow rate from 0.31 to 0.50 vvm gradually increased glutamic acid yield. Observing remarkable inhibitory effect of CO2 generated during fermentation some investigators (Richards, 1961 and Nyiri and Lengyal, 1965) have recommended for provision of ventilation in the unit operation of aeration and agitation.
Aeration- agitation condition should therefore be estimated properly for scale up of submerged fermentations in which CO2 was inhibitory. The rate of aeration is to be established to make sufficient ventilation and overcome this inhibition. A procedure of estimating aeration-agitation condition in fermentation considering both oxygen supply and ventilation is provided by Ishizaki and his associates (1973). This procedure was used in inosine fermentation. Inhibition of product formation and resistance to oxygen transfer pathway by CO2 is not clearly understood. However, the pathways of oxygen and CO2 as shown by Humphrey (1968) indicate that product inhibition by C02 might be due to (i) its action as a metabolic poison or (ii) the reduction of partial pressure of oxygen in the system thereby reducing its availability.
6. Suspended solids:
Presence of suspended cells or insoluble substrates might influence on oxygen transfer property in the liquid. In order to relate the rate of oxygen transfer measured in mixed liquor (in activated sludge) to that in a clean water Lister and Boon recommended a factor of proportionality given by
A decreasing ratio of KLa with increasing cell concentration at different agitational intensity was noticed in a n-parafin hydrocarbon fermentation (Mimura, 1973). It was believed that air bubbles covered with large number of cells resulted in a lower KL than with normal bubbles. Also available interface area (a’) between air and liquid where
in which β’ = (1/4 pc fc Dc = constant) indicates that the bubble size (Db), cell concentration Cx and air bubble hold up volume (Vb) in the liquid are important in computation of a’. Also, Mukhopadhyay and Ghose (1976) observed a decrease of KLa with increase in Ps. ovalis B 1486 cell concentration beyond 4.0 g l-1 in their studies in HRF. It was believed that this decreasing effect was probably due to overcrowding of cells in the film of liquid.
7. Bubble size and ionic strength:
Decrease in bubble diameter exposes greater surface area for transfer of gas from the bubble into liquid thus increasing KLa value. Benedeck and Heideger (1971) in the range of bubble size of 0.1 cm < dsm < 0.4 cm observed a linear relation between KL and dsm (souter-mean bubble diameter) as given below:
KL – 0.171 dsm – 0.0043 (5.60)
This equation predicts the influence of dsm or KL within limited range of dsm and indicates that in computation of KLa factors influencing bubble size distribution should be given importance. Ionic strength in the liquid is such a factor that can appreciably decrease bubble size (Calderbank, 1967; Marruci & Nicodeino, 1967 and Robinson & Wilke, 1973) even though the physico-chemical properties of the liquid remain essentially same. Fermentation liquid usually contains many ionic, mineral components. The ionic strength, T in the liquid is defined as (Robinson & Wilke, 1973)
Where Z; is the charge on an ionic species and C; is its concentration. In actual soluble substrate fermentation containing electrolytes a generalized correlation of KLa was obtained by Robinson and Wilke (1973) as below
In these equations e denotes KLa or KLr a/Ө where a is effective over all volumetirc mass transfer coefficient with reaction and Ө = (KLr/KL) is dimensionless absorption factor for mass transfer with chemical reaction, A. is a proportionality constant, m and n are exponents dependent on ionic strength of the liquid. Equation (5.62) expresses the dependency of KLa on ionic strength along with other physico-chemical parameters as ξ is dependent on density (pL), viscosity (μL), surface tension (σ) and DL of the liquid.
Ionic solutes in the liquid decrease average bubble size and increase dispersed gas fractional hold up. The gas hold up influences on KLa in the way as explained by Topiwala (1974).
8. Evaporation:
Water evaporation during fermentation that prolongs several days can effect on oxygen transfer coefficient (Aiba et al., 1973). Available information for elucidation of evaporation effect on KLa is scanty. The graphical correlation between oxygen transfer coefficient and water evaporation through the closure in shake flask is given in the book by Aiba et al. (1973). From this relation two possibilities might be assumed.
First, evaporation might decrease oxygen absorption rate by increasing the solute concentration in the liquid. Second it might increase OTR due to greater partial pressure of oxygen inside the enclosure. However, which one of the two facts will be predominant depends on the system characteristics. Nowadays in bench scale bioreactors asceptic cold finger has been installed to prevent evaporation loss.
9. Surface Aeration:
Fuch et al. (1971) determined the effect of surface aeration on KLa with air-water systems in different size of fermenters (Table 5.8) in order to include surface aeration in scale up. Power factor, NP, defined as has great relevance to surface aeration. Here denotes a function. Other symbols have the same significance as used earlier.
NP = (N3 Di5/V) (5.64)
Variation of KLa as a function of NP showed a general trend towards decreasing KLa of surface aeration for smaller values of NP as the fermenter size increases. It showed that a contribution of surface aeration on KLa generally increases as fermenter size decrease (Table 5.8). Surface aeration KLa is shown to be related to (P/V) ratio as in which σj is dependent of Np. Oxygen transfer on the basis of unit volume of liquid and per unit cross sectional area also shows the increasing trend of surface aeration KLa with decreasing fermenter size.