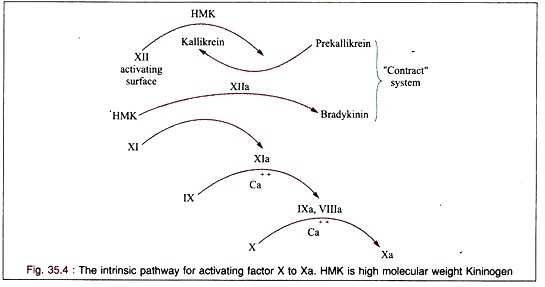
If a container is filled with a suspension of particles of varying size and density, the particles will gradually settle to the bottom of the container under the influence of gravity.
The rate at which settling occurs can be greatly increased by increasing the gravitational effect on the particles. This is the rationale behind the use of centrifugation.
A tube containing a suspension of particles (e.g., a tissue homogenate) is placed in the rotor of a centrifuge and then is rotated at high speed.
The resulting acceleration greatly increases the force acting on the suspended particles, causing their more rapid sedimentation to the bottom of the tube along paths that are perpendicular to the axis of rotation (i.e., along radii of the circle being swept out by the rotating tubes; see Fig. 12-1).
Although the practical application of centrifugal force can be traced back more than a thousand years, the modern era of centrifugal methodology began in the early years of this century when the focal point of biochemistry was the study of the chemical and physical properties of protein solutions and other colloids. The discovery by Emil Fischer in 1902 that proteins consisted of long chains of amino acids turned out to be the main impetus behind a dramatic surge in the development of centrifugal methods.
Fischer and most other notable chemists of the period believed that individual protein species (myoglobin, hemoglobin, etc.) were polydisperse; that is, a given protein type was believed to occur in various sizes (i.e., various polypeptide chain lengths). That this is not the case was shown by Theodor Svedberg, who developed the first “analytical ultracentrifuges” (see below), in which the movements of sedimenting particles can be followed optically.
Svedberg showed that a given protein type is not polydisperse but is homogeneous (or mono-disperse), with all molecules of that protein having the same, well-defined molecular weight. In 1926, Svedberg received the Nobel Prize in recognition of his pioneering centrifugal studies of proteins and other colloids.
Theory of Centrifugation:
The force acting on a particle during centrifugation is given by the equation:
F = mω2x (12-1)
Where to is the mass of the particle, ω (omega) is the angular velocity of the spinning rotor in radians per second (one unit of circumference contains 2π radians), and x is the distance of the particle from the axis of rotation.
Usually, the value given for the force applied to particles during centrifugation is a relative one; that is, it is compared with the force that the earth’s gravity would have on the same particles. It is called relative centrifugal force or RCF and is given by
Where g is acceleration due to gravity and equals 980 cm/sec/sec.
Because g is a constant, then
In equation 12-3, the term (27r/60)/980 is also a constant and is equal to 1.119 x 10-5.
Thus the equation for relative centrifugal force (i.e., equation 12-2) simplifies to
RCF = 1.119 x 10-5 (rpm)2 (12-4)
Consequently, to determine the relative centrifugal force in effect during centrifugation it is necessary to measure the revolutions per minute (rpm) of the rotor and the distance between the sample and the axis of rotation. Because RCF is the ratio of two forces, it has no units. However, it is customary to follow the numerical value of the RCF with the symbol g. This indicates that the applied RCF is a multiple of the earth’s gravitational force.
Sample Problem:
What is the maximum relative centrifugal force applied when red blood cells are sedimented at 1000 rpm in a rotor of maximum sample radius equal to 10 cm?
RCFmax = 1.119 x 10-5 (1000)2(10)
= 1.119 x 102 or 112g
The sedimentation of particles by centrifugation is, in effect, a method for concentrating them; therefore, one of the major physical forces opposing such concentration is diffusion. In the case of the sedimentation of cells or sub-cellular organelles (nuclei, mitochondria, etc.), the effects of diffusion are essentially nil. However, when centrifugation is used to sediment much smaller particles (such as cellular proteins, nucleic acids, or polysaccharides), the effects of diffusion become significant.
Sedimentation Rate and Sedimentation Coefficient:
The RCF or “g force” applied to particles during centrifugation may readily be calculated using equation 12-4 and is independent of the physical properties of the particles being sedimented. However, a particle’s sedimentation rate at a specified RCF depends on the properties of the particle itself.
Also, because the RCF varies directly with x, it is clear that the sedimentation rate changes with changing distance from the axis of rotation. (For particles settling under the influence of the earth’s gravity alone, the sedimentation rate is constant.)
The instantaneous sedimentation rate of a particle during centrifugation is determined by three forces:
(1) FC, the centrifugal force,
(2) FB, the buoyant force of the medium, and
(3) FF, the frictional resistance to the particle’s movement.
Equation 12-13 is very important to the understanding of particle sedimentation and should be carefully examined, for the equation shows that those properties of a particle that determine its rate of sedimentation during centrifugation are radius and effective density (i.e., the difference between the density of the particle and the density of the liquid through which the particle is sedimenting).
Because the sedimentation rate varies in proportion to the square of the particle’s radius (but is a first-order function of the particle’s density) it is clear that particle size is “more influential” than particle density in determing sedimentation rate.
From equation 12-13, it may also be noted that two particles having different sizes or different densities can have similar sedimentation coefficients. On the other hand, two particles with either similar size or similar density can have markedly different sedimentation coefficients.
The Analytical Ultracentrifuge:
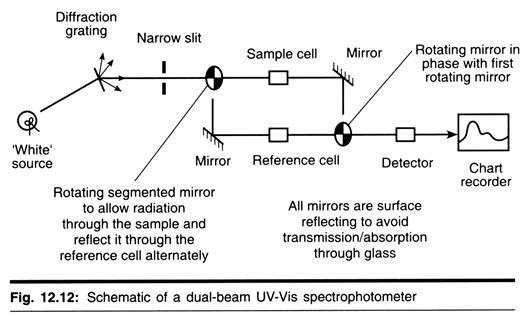
The sedimentation coefficient of a particle may be determined experimentally using an instrument known as an analytical ultracentrifuge. The rotor that spins in this ultracentrifuge typically contains two compartments. Into one compartment is placed a “reference cell” containing sample-free solvent and the other receives a cell containing the sample to be analyzed. The interior of each cell is sector shaped and bounded above and below by parallel quartz windows to permit light from below the rotor to pass through the reference and sample during rotation (Fig. 12-2).
As the particles sediment, boundaries are formed at the trailing edges of each particulate species. Changes in the distance between each boundary and the axis of rotation are measured as a function of time by the instrument’s optical system.
These measurements are then used to calculate the respective sedimentation coefficients of the particles in the suspension. The sharpness of the boundaries that are formed serves as an index of the heterogeneity of the sample. The first analytical ultracentrifuges were designed and built by T. Svedberg in the 1920s.
The sedimentation coefficients of many cellular macromolecules such as proteins and nucleic acids fall in the range of 1 x 10-13 to 200 x 10-13 seconds (i.e., the dimensions of s are seconds). For convenience, a unit called the Svedberg unit (named in honor of T. Svedberg), abbreviated S, is used to describe sedimentation coefficients and is equal to the constant 10-13 seconds. Thus, most cellular proteins have sedimentation coefficients between 1 and 200 S. The sedimentation coefficients of a number of cell constituents are listed in Table 12-1.
Calculation of the sedimentation coefficient from data collected with the analytical ultracentrifuge involves the following amplification of the relationship of equation 12-12. If a boundary is x1 centimeters from the axis of rotation at time t1 and x2 centimeters at time t2, then equation 12-12 may be solved by integration as follows. First, by transposition,
Sample Problem:
A solution containing a single particulate species is accelerated in the analytical ultracentrifuge at 60,000 rpm. At time t1; the boundary between the trailing edge of the sedimenting particles and the axis of rotation is 6.0 cm, while at t2, 60 minutes later, the boundary is 6.8 cm from the axis. What is the sedimentation coefficient of the particles?
As its name implies, the analytical ultracentrifuge is an instrument for analysis and does not physically separate the multiple components of a mixture from one another. Furthermore, the amount of material that may be studied is quite limited as a result of the small size of the rotor’s sample cell.
Preparative Centrifugation:
The counterpart to analytical centrifugation is preparative centrifugation, which provides for the isolation of cell components for further analysis. Two basic types of centrifuge rotors are regularly employed for conventional preparative centrifugation; these are the swinging-bucket rotor and the fixed-angle rotor (Fig. 12-3).
The swinging-bucket rotor consists of a series of metal buckets attached to the central harness of the rotor. The samples to be centrifuged (previously placed in centrifuge tubes) are inserted into the buckets, which swing upward from a vertical position to a horizontal position during acceleration of the rotor (Fig. 12-3).
During deceleration, the buckets return to the vertical position and the centrifuge tubes are then removed. In a fixed-angle rotor, the centrifuge tubes are maintained at a constant angle (usually 15° to 45° from verticality) throughout centrifugation (Fig. 12-3). As a result, the radially sedimenting particles quickly strike the tube wall, where convection currents help to carry them to the bottom of the tube.
Differential Centrifugation:
During centrifugation, particles sediment through the medium in which they are suspended at rates related to their size, shape, and density. Differences in the sedimentation coefficients of the various subcellular particles provide the means for their effective separation.
Differential centrifugation, a technique introduced to cellular research in the early 1940s by the noted biologist and Nobel laureate Albert Claude, is one of the classic procedures for isolating subcellular particles and involves the stepwise removal of classes of particles by successive centrifugations at increasing RCF.
The material to be fractionated is subjected first to low-speed centrifugation to sediment the largest (or densest) particles present. Following this, the unsedimented material (called the supernatant) is transferred to another tube and centrifuged at a higher speed (and usually also for a longer period of time) to sediment particles of somewhat smaller size (and/or lower density).
The sequence is repeated several times until all particles have been sedimented; each sediment is then used for further experimentation and analysis. The procedure that is routinely used for the differential fractionation of liver tissue serves as a convenient example of this method and is shown diagrammatically in Figure 12-4.
The removed liver tissue is homogenized in cold buffer and centrifuged 10 minutes at 700 g. This is usually sufficient to sediment all the cell nuclei to the bottom of the centrifuge tube, thereby providing the nuclear fraction. Depending on the effectiveness of the homogenization procedure, some unbroken cells and large cell fragments may also be recovered in this fraction.
The overlying supernatant (called the nuclear supernatant) is removed and transferred to another tube for a second centrifugation at 20,000 g for 15 minutes. These sediments nearly all the mitochondria (i.e., the mitochondrial fraction).
Again, the supernatant (i.e., mitochondrial supernatant) is removed and is subjected to a third centrifugation at 105,000 g for 60 minutes. This causes the sedimentation of a fraction called microsomes, which includes ribosomes and small fragments of intracellular membranes.
The microsomal supernatant is referred to as the soluble phase of the cells, or cytosol, and includes soluble proteins, soluble nucleic acids, soluble polysaccharides, lipid droplets, and other minute particles. In the procedure just described the liver tissue is separated into four major fractions.
Markers:
The most widely used methods for identifying the constituents of fractions produced by centrifugation involve microscopy and chemical and bioassays for specific markers. Although the light microscope may be used to successfully identify the larger cellular structures such as nuclei, chloroplasts, and mitochondria, the identification of smaller particles such as peroxisomes and ribosomes requires electron microscopy.
Certain enzymes and other molecules may be peculiarly associated with a particular cell component and therefore readily serve as markers. For example, the enzyme succinic dehydrogenase is found exclusively in mitochondria; consequently, any centrifugal fraction that exhibits succinic dehydrogenase activity would be expected to contain mitochondria.
Chloroplast-rich fractions exhibit ribulose diphosphatase activity, plasma membrane-rich fractions exhibit adenylate cyclase activity, and so on. Table 12-2 lists some of the more useful and reliable markers used in the identification of the components present in the tissue and cell fractions produced during centrifugation. It should be noted that not all markers are enzymes; DNA is an excellent marker of nuclei-rich fractions and chlorophyll is an excellent chloroplast marker.
Differential centrifugation has several major disadvantages. Because the homogenate is initially distributed uniformly throughout the centrifuge tube, the first particles sedimented will necessarily be contaminated with small amounts of all other constituents of the homogenate. This effect is shown in Figure 12-5.
As the smaller particles are sedimented, they in turn will be contaminated by even smaller particles. In fact, the only particles obtained in relatively pure form will be those that sediment most slowly. In the example given above, the initial nuclear fraction would contain some mitochondria, microsomes, and cytosol; the mitochondrial fraction obtained in the second centrifugation would be contaminated with microsomes and cytosol, and so on.
These disadvantages may not be serious in some instances, because the major subcellular particles of a tissue homogenate have sedimentation coefficients that differ from one another by one or more orders of magnitude. However, serious difficulties arise if the particles to be separated have similar sedimentation coefficients. This problem is illustrated in Figure 12-4f, in which the mitochondrial fraction also contains the cells’ lysosomes.
Density Gradient Centrifugation:
The resolution achieved during centrifugation can be greatly improved if the mixture of particles is confined at the outset to a narrow zone at the top of the centrifuge tube and the particles then permitted to sediment from this position.
Initial stability under these conditions can be obtained only if the particles are layered onto a density gradient, that is, a column of fluid of increasing density. This technique, known as density gradient centrifugation, was introduced to cellular research in the late 1940s and early 1950s by N. G. Anderson and M. K. Brakke and is an exceedingly powerful preparative tool.
Density gradients may be stepwise (discontinuous) or continuous. A step gradient is prepared by successively layering solutions of decreasing density in the centrifuge tube. Continuous density gradients are prepared by mixing dense and light solutions in varying proportions at a controlled rate and delivering the mixture to a centrifuge tube in a continuous stream.
A simple procedure for producing a “linear” density gradient is shown in Figure 12-6. In this procedure, the light solution (in the right cylinder) flows into and is mixed with the dense solution (in the left cylinder).
The mixture is then delivered to the centrifuge tube. Using this method, a density gradient is formed that decreases linearly as a function of volume between the limiting densities originally present in the two cylinders.
Gradients with other shapes (exponential, hyperbolic, etc.) may be prepared using containers of various non-cylindrical shapes or gradient- generating devices specifically manufactured for this purpose. Solutes used to provide solutions for density gradients are selected on the basis of their solubility in water and their compatibility with cells and subcellular organelles.
Sucrose, Ficoll (a copolymer of sucrose and epicholorhydrin), Metrizamide, Nycodenz, and Percoll (a colloidal form of silica) are the most popular, as they have minimal detrimental effects on organelles and provide densities up to about 1.3 g/cm Cesium chloride, cesium trifluoroacetate, and other dense salts are used when the limiting density must be considerably higher (i.e., up to 1.9 g/cm). The rate at which particles sediment through a density gradient is given by equation 12-13. Because the quantity (ρP – ρM) changes as the particles sediment deeper into the gradient, s also changes.
If a particle reaches a position in the gradient where the particle’s density and the gradient’s density are the same (i.e., ρP = ρM), then s becomes zero, and no further sedimentation of the particle occurs. If a particle suspension is overlaid with a gradient whose maximum density is greater than that of the particles (i.e., ρM > ρP), then during centrifugation the particles will rise through the gradient, for when ρM is greater than ρP, s becomes a negative term.
Rate Sedimentation:
When the densest region of a density gradient (i.e., the liquid at the bottom of the centrifuge tube) is less dense than the particles being sedimented, all particles will eventually reach the bottom of the tube (if centrifugation is continued long enough).
However, if the duration of centrifugation is carefully limited, this will not occur; instead, the particles will be distributed through the density gradient in the order of their sedimentation coefficient. Fractionations carried out in this manner are called rate separations and are based on the combined contributions of particle size and particle density. The rate fractionation of a liver tissue homogenate is depicted in Figure 12-7. The four major cell fractions (nuclear, mitochondrial, microsomal, and cytosol) are separated during a single centrifugation.
Isopycnic Sedimentation:
When the densest region of a density gradient is denser than any of the particles to be sedimented, none can reach the bottom of the tube regardless of how long centrifugation is carried out. Instead, the particles will sediment through the gradient until they reach their isodense or isopycnic position.
Fractionations carried out on the basis of particle density alone are called isopycnic separations. It is to be noted that this implies that small, dense particles with low sedimentation coefficients sediment further through such a density gradient than large, light particles with high sedimentation coefficients (Fig. 12-8).
In rate separations, both particle size and particle density determine the final positions of particles in the gradient. However, of the two parameters, size is more influential because s is a second-order function of particle radius but a first-order function of particle density. In isopycnic separations, particle density alone determines final position in the density gradient. Figure 12-9 compares the sedimentation coefficients and densities of a variety of cellular components.
In certain instances, it is not necessary to layer the sample to be fractionated onto a preformed density gradient. Instead, the sample and the density gradient solutions are mixed and placed in the centrifuge tube. During centrifugation at high speed, the density gradient forms automatically within the tube, and particles migrate (upward and/or downward) to their isopycnic positions. This procedure is known as equilibrium isopycnic centrifugation and is regularly carried out using solutions of CsCl or other heavy salts (Fig. 12-10).
Although density gradient centrifugation is usually carried out in swinging-bucket rotors, isopycnic (but not rate) separations can also be performed in fixed- angle rotors (Fig. 12-11a). When the gradient with sample layered above is placed in the inclined position in the rotor, the sample zone and equal density planes within the gradient form ellipses.
During acceleration of the rotor, each isodense elliptical layer becomes a small section of a paraboloid of revolution with focal point on the axis of rotation. The family of paraboloids becomes increasingly steep as rotor acceleration continues and eventually approaches vertically; this phenomenon is called gradient reorientation.
Particles in the gradient sediment radially until they encounter the sloping tube wall; from there, they are carried down through the gradient by centrifugal force and convection until they reach the isodense region of the gradient, where they form layers. Rotor deceleration reorients the gradient again so that the separated particles form horizontal layers.
A recent modification of the fixed-angle approach to isopycnic centrifugation involves the use of vertical tube rotors in which the fixed angle is reduced to 0 (i.e., the centrifuge tubes are maintained in the vertical position throughout; Fig. 12-11b). Here, too, the gradient is reoriented during rotor acceleration and deceleration.