The following points highlight top four main types of sampling schemes that are applied in microbiological testing of food. The types are:- 1. Two-Class Attributes Plans 2. Three-Class Attributes Plans 3. Choosing a Plan Stringency 4. Variables Acceptance Sampling.
Type # 1. Two-Class Attributes Plans:
In an attributes sampling scheme analytical results are assigned into classes; in the simplest type, the two-class scheme, samples are classified as acceptable or defective depending on the test result. A sample is described as defective if it is shown to contain more than a specified number of organisms or in cases where a presence or absence test is applied, the target organism is detected.
A two-class sampling scheme is defined by three numbers:
n – the number of sample units to be tested;
m – the count above which the sample is regarded as defective. This term would not appear in schemes employing a presence/absence test since a positive result is sufficient for the sample to be defective;
c – the maximum allowable number of sample units which may exceed m before the lot is rejected.
Such schemes do not make full use of the numerical data obtained but simply classify sample units according to the test result.
For example, if m is 104 cfu g-1, those samples giving counts of 102, 9 x 103, and 1.2 x 104 would be considered acceptable, acceptable, and defective respectively, despite the fact that the first sample had a count almost 2 log cycles lower than the second and the difference in count between the second and third samples is relatively small.
Using this approach, results from a number of sample units can be classified according to the proportion defective and the frequency of occurrence of defective units described by a binomial distribution.
If p represents the proportion of defective sample units in the whole lot, i.e. the probability of a single sample unit being defective, and q represents the proportion of acceptable units (the probability of a sample unit being acceptable), then the probability distribution of the various possible outcomes is given by the expansion of the binomial:
(p + q)n —————– (11.1)
Where n, the number of sample units examined, is small compared with the lot size. Since, in a two-class plan, a sample can only be acceptable or defective then
p + q = 1 —————— (11.2)
The probability that an event will occur x times out of n tests is given by:
P(x) = (n!/(n – x)! x!) px q(n – x) —————(11.3)
or if we substitute (1 — p) for q:
P(x) = (n!/(n – x)! x!) px (1 – p)n – x —————(11.4)
If we have a sampling plan which does not permit any defective samples (c = 0), then by putting x = 0 into Equation (11.4) we obtain an expression for the probability of obtaining zero defective samples, i.e. the probability of accepting a lot containing a proportion p defective samples:
Pacc = (1 – p)n ———– (11.5)
It follows that the probability of rejection is:
Prej = 1 – (1 – p)n ——— (11.6)
We can use this equation to determine how effective such relatively simple sampling schemes are. For example, Table 11.1 shows how the frequency (probability) of finding a defective sample changes with the level of defectives in the lot as a whole and with the number of samples taken: This could apply to a Salmonella-testing scheme where detection of the organism in a single sample is sufficient for the whole lot to be rejected.
If the incidence of Salmonella is 1% (p = 0.01), a level corresponding to 40 positive 25 g samples in a lot of 1 tonne (4000 x 25g samples), then the lot would be accepted 90% of the time if 10 samples were tested on each occasion.
When the number of samples taken at each testing is increased then the chances of rejection are increased, so that with 20 samples the lot would be accepted 82% of the time. If we went to testing 100 samples, we would accept the same lot only 37% of the time.
A statistically equivalent situation would be the testing of an appertized food for the presence of surviving organisms capable of spoiling the product, and where detection of one defective pack would mean rejection of the lot.
Using Table 11.1 again, we can see that if there was a failure rate of one pack in a thousand (p = 0.001), even taking 100 packs for microbiological testing we would only reject a lot on one out of ten occasions.
In fact we can calculate the number of packs it would be necessary to take in order to have a 95% probability of finding one defective sample (Prej = 0.95). This is done simply by substituting in Equation (11.6) and solving for n. The answer, 2995, demonstrates why it is necessary to have alternatives to microbiological testing to control the quality of appertized foods.
The probabilities of acceptance or rejection associated with an attributes sampling plan can be calculated from the binomial distribution. For large batches of product these can also be represented graphically by what is known as an operating characteristic (OC) curve of the type shown in Figure 11.2. For each level of defectives in the lot, the probability of its acceptance or rejection using that plan can be read off the curve.
Figure 11.3 demonstrates that as n increases for a given value of c, the stringency of the plan increases since a lot’s overall quality must increase with n for it to have the same chance of being passed. If c is increased for a given value of n (Figure 11.4), so the plan becomes more lenient as lot quality can decrease but still retain the same chance of being accepted.
The ideal OC curve would resemble Figure 11.5 with a vertical cut off at the maximum acceptable level of defectives. To achieve this would require testing an unacceptably high number of samples so the purchaser has to adopt a sampling plan which will accept lots defined as being of good quality most (e.g. 95%) of the time and has a high probability (e.g. 90%) of rejecting lots of poor quality (Figure 11.6).
Two types of error are identifiable in this approach: the producer’s risk that a lot of acceptable quality would be rejected (5%), and the consumer’s or purchaser’s risk that a lot of unacceptable quality would be accepted (10%). Lots of intermediate quality would be accepted at a frequency of between 10 and 95%.
Type # 2. Three-Class Attributes Plans:
Three-class attributes sampling plans introduce a further category and divide samples into three classes: acceptable, marginally acceptable, and unacceptable. Use of this extra classification of marginally acceptable means that they are not used with presence or absence tests but only with microbiological count data.
A three- class plan is defined by four numbers:
n – the number of samples to be taken from a lot;
M – a count which if exceeded by any of the test samples would lead to rejection of the lot;
m – a count which separates good quality from marginal quality and which most test samples should not exceed;
c – the maximum number of test samples which may fall into the marginally acceptable category before the lot is rejected.
As with the two-class plan increasing c or decreasing n increases the leniency of a three-class plan. OC curves for three-class plans can be derived from the trinomial distribution and describe a 3-dimensional surface with axes defining the probability of acceptance/rejection, the proportion of marginally defectives in a lot, and the proportion of defectives in a lot (Figure 11.7).
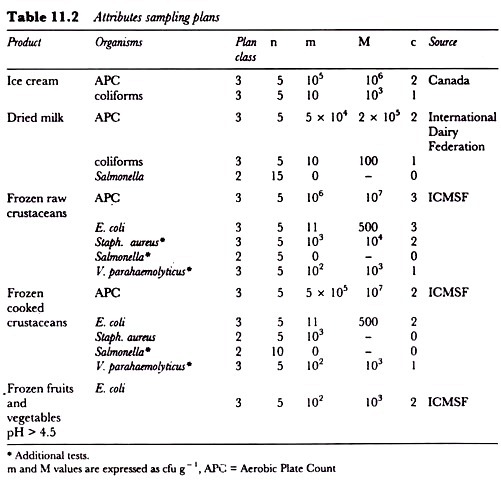
Microbiological criteria using attributes sampling plans for different foods have been produced by a number of organizations and some examples of these are given in Table 11.2. As is clear, the stringency of the sampling plan varies with the type of food and the organism being sought.
 Type # 3. Choosing a Plan Stringency:
Type # 3. Choosing a Plan Stringency:
Two important principles governing the choice of plan stringency are presented in Table 11.3. As the severity of the hazard being tested for increases, so too must the stringency of the sampling plan. For example, spoilage can be regarded as more of a risk to the product than to the consumer and so tests for indicators of shelf-life such as aerobic plate counts will have the most lenient sampling plans.
Even though such plans may quite frequently pass products which are defective, they can still be effective in the sense that regular rejection of say 1 in 5 batches of product would represent a significant economic loss to the producer and would be a strong incentive to improve quality.
Interpretation of the significance of high numbers of indicator organisms will depend on the indicator and the food involved. Enterobacteriaceae or coliform counts can provide an indication of the adequacy of process hygiene, though they are naturally present in substantial numbers on several raw foods.
Escherichia coli is indicative of faecal contamination and the possible presence of enteric pathogens, although there is no direct relationship and interpretation is not clear-cut. Because of these uncertainties, indicator tests are of only moderate stringency.
When looking for known pathogens, more stringent sampling plans are appropriate and these become more demanding as the severity of the illness the pathogen causes increases. The conditions under which the food is to be handled after sampling must also be accommodated in any plan.
For example, a sampling plan for E. coli in raw meats can be quite lenient since the organism is not uncommon in raw meats and the product will presumably be cooked before consumption, thus reducing the hazard.
A more stringent plan is required for the same organism if the subsequent handling of a food will produce no change in the hazard; for example, ice cream which is stored frozen until consumption. The most stringent plan would be required for products where subsequent handling could increase the hazard.
This would be the case with dried milk where the product could be reconstituted and held at temperatures which would allow microbial growth to resume. Plan stringency should also take account of whether the food is to be consumed by particularly vulnerable groups of the population such as infants, the very old, or the very sick.
Type # 4. Variables Acceptance Sampling:
Very often we have no idea how micro-organisms are distributed within a batch of food and have no alternative but to use an attributes sampling scheme which makes no assumption on this question. In many cases though, studies have found that micro-organisms are distributed Jog-normally, that is to say the logarithms of the counts from different samples conform to a normal distribution.
For example, a survey of nearly 1300 batches of frozen and dried foods found that, on average, only 7.8% of batches did not conform to a log-normal distribution.
When this is the case it is possible to use a variables acceptance sampling procedure which achieves better discrimination by making full use of the numerical data obtained from testing rather than just assigning test results into classes as is done in sampling by attributes.
The shape of a normal distribution curve is determined by the parameters σ, the population mean which determines the maximum height of the curve, and a, the standard deviation of the distribution which determines its spread.
For any log count V in a log-normal distribution, a certain proportion of counts will lie above V determined by:
(V= µ) / σ (=K) —————– (11.7)
where K is known as the standardized normal deviate.
For example, when:
K= 0 (V= µ) then 50% of values will lie above V;
K= 1 (V= µ + σ) then 16% of values lie above V;
K- 1.65 (V= n + 1.65 σ) then 5% of values lie above V.
Rearranging, we get:
µ + Kσ = V —————– (11.8)
If V is chosen to represent a log count related to a safety or quality limit and K determines the acceptable proportion of samples in excess of V then a lot would be acceptable if:
µ + Kσ ≤ V —————–(11.9)
and unacceptable if:
µ + Kσ > V —————–(11.10)
In practice V is likely to be very close to the logarithm of M, used in three-class attribute plans. Since we do not know µ or σ, we must use estimates derived from our testing, x, the mean log count, and s, the sample standard deviation.
K is replaced with a value k1, derived from standard Tables, which makes allowance for our imprecision in estimating K and chosen to give a desired lowest probability for rejection of a lot having an unacceptable proportion of counts greater than V.
This gives us the condition for rejection:
x̅ + k1s > V ————–(11.11)
Some k1 values are presented in Table 11.4. If we decrease the desired minimum probability of rejection for a given proportion exceeding V, i.e. decrease the stringency of the plan, then k1 decreases. Application of a variables plan for control purposes will give a lower producer’s risk than the equivalent attributes scheme.
It is possible to apply the variables plan as a guideline to Good Manufacturing Practice (GMP).
In this case the criterion is:
x̅ + k2s < v —————(11.12)
where k2 is derived from Tables and gives a certain minimum probability of acceptance provided less than a certain proportion exceeds v a lower limit value characteristic of product produced under conditions of Good Manufacturing Practice (Table 11.4).
The value v will be very similar to the logarithm of m used in the three-class attributes plan. If a lot were to fail a GMP criterion it would not lead to rejection of the lot but would alert the manufacturer to an apparent failure of GMP.
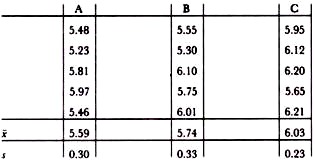
If we take a practical example, let us assume that the critical safety/quality limit is 107 cfu g_1 (V = 7), but that under conditions of GMP a level below 106 is usually attainable (v = 6). We are testing five samples from the lot and wish to be 95% certain to reject lots where more than 10% of samples exceed a count of 107. From Table 11.4, k1 = 3.4 and our specification becomes:
if X̅ + 3.4s > 7 then reject.
If we also wish to be 95% sure of acceing lots with less than 20% greater than our GMP limit then from Table 11.4, k2 is 0. 11 and our GMP criterion becomes:
if X̅ + 0.11s < 6 then accept.
Three batches of product give the following log counts:
Applying the safety/quality limit and GMP formulae, batches A and B are acceptable according to both criteria. Batch C, though acceptable with respect to the safety/quality limit, is not acceptable according to the GMP criterion and this may warrant further investigation.