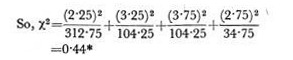A very important use of biometry in the field of genetics is for testing goodness of fit. The testing is done by two methods. They are: (1) The Standard Error Method and (2) The Chi-square Method.
A very important use of biometry in the field of genetics is for testing whether a particular ratio of observations may be taken to fit to an expected ratio. For example, we expect that a monohybrid ratio should be 3:1 but perhaps the actual result obtained from an experiment is 2.85: 1. Should we accept this different ratio to be within ordinary limits of error? Such deviations from the expected ratio are bound to occur in all such experiments as accidents will always happen with living organisms. It is, therefore, always necessary to test if the deviation is within reasonable limits.
This is known as Testing Goodness of Fit which may be done by two methods:
Method # 1. The Standard Error Method:
This is quite a good process when the ratio between two classes only (e.g., the monohybrid 3: 1 ratio) is to be tested. The standard error of the ratio is obtained by the formula
when p is one of the expected percentages (conveniently expressed as a decimal) and q the other (i.e., 1—p) while n is the total number. Deviation is the difference between an expected value and the value obtained.
Results obtained are usually taken to be a good fit to a ratio so long as deviation/S.E.r is less than 2.
Let us taken an example. In the T x d cross, Mendel obtained 787 tails and 277 dwarfs—a total of 1064. The ratio obtained is 0 74: 0 26 while the expected ratio is 0-75: 0-25 (3: 1). Therefore, the deviation is 0 75-0-74 = 0 01. Then by the above formula
(i.e., less than 2) so that the result may be taken to conform to the 3:1 ratio.
Method # 2. The Chi-square Method:
Chi-square (named after the Greek letter x) is a method which can be used for various types of biological problems and is, therefore, much more useful than the standard error method.
Without going into the reasoning, it is quite convenient to use the following formula mechanically:
X2 = ∑ d2/e which is a summation of the square of the deviation in each class (d2) divided by the expected number (e) for each class.
An example will clarify its use. Let us take Mendel’s T x d cross again. The observed numbers were 787 and 277 while the expected numbers, in order to conform exactly to the 3:1 ratio, ought to be 798 and 266. Then, considering the two classes (3 and 1, i.e., T and d)—
Now it has to be tested if the value of X2 obtained fits to a 3:1 ratio. For that we are to consult the short table below:
Degree of freedom means the number of alternative classes which will be one less than the number of actual classes. So, for a 3: 1 ratio the d-f is 1; for 9: 3: 3: 1 d.f. is 3. The right-hand column shows the probability of obtaining a higher value of x2 as a result of chance alone if the sample is from a population conforming to the particular ratio. Looking at the table we find that the X2 of 0.61 obtained has P between 0.50 and 0.05 that is, the probability of obtaining a value higher than this is much greater than 0.05 or 5% or 5 times in 100 trials.
So, the result obtained is a very good fit (marked by an asterisk) to the 3: 1 ratio. Values showing P > 0.05 (i.e., above 5% level) are considered good fit and higher the value of P (i.e., smaller the chi-square) better is the fit. It should be remembered that in statistical experiments, the conclusions are reliable only when the number of individuals (n) considered is reasonably large. Segregation ratios involving fewer individuals may show good fit to 2 or 3 different ratios rendering the conclusion doubtful.
For the dihybrid ratio, Mendel obtained 315, 101, 108 and 32 plants, while, for a 9:3:3:1 ratio the expected number are 312.75, 104.25, 104.25, and 34.75.
which is much less than the maximum limit for 3 d.f. So this is also a very good fit.