Decay by Negatron Emission:
In this case a neutron is converted to a proton by the ejection of a negatively charged beta (β) particle called a negatron (β–)
neutron → proton + negatron
To all intents and purposes a negatron is an electron, but the term negatron is preferred, although not always used, since it serves to emphasise the nuclear origin of the particle. As a result of negatron emission, the nucleus loses a neutron but gains a proton. The N/Z ratio, therefore, decreases while Z increases by 1 and A remains constant. An isotope frequently used in biological work that decays by negatron emission is 14C.
146C → 147N + β–
Negatron emission is very important to biochemists because many of the commonly used radionuclides decay by this mechanism. Examples are; 3H and 14C, which can be used to label any organic compound, 35S used to label methionine, for example, to study protein synthesis; and 32P, a powerful tool in molecular biology when used as a nucleic acid label.
Decay by Positron Emission:
Some isotopes decay by emitting positively charged β-particles referred to as positron (β+). This occurs when a positron is converted to a neutron.
proton → neutron + positron
Positrons are extremely unstable and have only a transient existence. Once they have dissipated their energy, they are intact with electron and are annihilated. The mass and energy of the two particles are converted to two у-rays emitted at 180° to each other. This phenomenon is frequently described as back to back emission.
As a result of positron emission the nucleus loses a proton and gains a neutron, the N/Z ratio increases, Z decreases by 1, and A remains constant. An example of an isotope decaying by positron emission is 22Na:
2211Na → 2210Ne + β+
Positron emitters are detected by the same instruments used to detect у-radiation. They are used in biological sciences to spectacular effect in brain scanning with the technique positron emission tomography (PET scanning) used to identify active and inactive areas of the brain.
Decay by Alpha-particle Emission:
Isotopes of elements with high atomic numbers frequently decay by emitting alpha (α)-particles. An α-particle is a helium nucleus; it consists of two protons and two neutrons (4He2+). Emissions of a-particle result in a considerable lightening of the nucleus, a decrease in atomic number of 2 and a decrease in the mass number of 4. Isotopes that decay by a-emission are not frequently encountered in biological work. Radium-226 (226Ra) decays by α-emission to radon-222 (222Rn), which is itself radioactive. Thus begins a complex decay series, which culminates in formation of 206Pb:
22688Ra → 42He2+ + 22286Rn →→→ 20682Pb
Alpha emitters are extremely toxic, if ingested, due to the large mass and the ionizing power of the atomic particle.
Electron Capture:
In this form of decay a proton captures an electron orbiting in the innermost K-shell;
proton + electron → neutron + X-ray
The proton becomes a neutron and electromagnetic radiation (X-rays) is given out. The process is called electron capture decay, or sometimes K capture because the captured electron comes from the innermost shell of orbiting electrons which is known as the K-shell. After this has taken place there will be an electron missing from the K-shell and so other electrons will immediately fall down to fill the vacancy, emitting characteristic X-rays as they do so.
In the same way the swapping of a proton for a neutron in the nucleus involves a change in the configuration of nucleons and the emission of the excess energy of the nucleus as gamma-rays. Iodine-125 is an example of a nuclide which decays by electron capture.
Decay by Emission of γ-rays:
In contrast to emission of α- and β-particles, γ-emission involves electromagnetic radiation similar to, but with a shorter wavelength than, X-rays. These γ-rays result from a transformation of a nucleus of an atom (in contrast to X-rays, which are emitted as a consequence of excitation involving the orbital electrons of an atom) and frequently accompany α- and β-particles emission. Emission of γ- rays in itself leads to no change in atomic number or mass.
γ-radiation has low ionizing power but high penetration. For example, the у-radiation from 60Co penetrates 15 cm of steel. The toxicity of y-radiation is similar to that of X-rays.
Example: 13153I → 13154Xe + β– + γ
Radioactive Decay Energy:
The usual unit used in expressing energy levels associated with radioactive decay is the electron volt. One electron volt (eV) is the energy acquired by one electron in accelerating through a potential difference of IV and is equivalent to 1.6 × 10-19 J). For the majority of isotopes, the term million or mega electron volt (MeV) is more applicable. Isotopes emitting a-particles are more normally the most energetic, falling in the range 4.0-8.0 MeV, whereas β and γ-emitters generally have decay energies of less than 3.0 MeV.
Rate of Radioactive Decay:
Radioactive decay is a spontaneous process and it occurs at a definite rate characteristic of the source. This rate always follows an exponential law. Thus the number of atoms disintegrating at any time is proportional to the number of atoms of the isotope (N) present at any time (t). Expressed mathematically, the exponential curve gives the equation.
-dN/dT αN
or,
-dN/dT = λN, …(13.1)
where λ is the decay constant, a characteristic of a given isotope defined as the fraction of an isotope decaying in unit time (t-1). By integrating equation 13.1, it can be converted to a logarithmic form:
In Nt/N0 = λt, …(13.2)
where Nt is the number of radioactive atoms present at time t, and N0 is the number of radioactive atoms originally present. In practice it is more convenient to express the decay constants in terms of half-life (t1/2). This is defined as the time taken for the activity to fall from any value to half that value. If Nt in equation 13.2 is equal to one-half of N0 then t will equal the half-life of the isotope
Thus
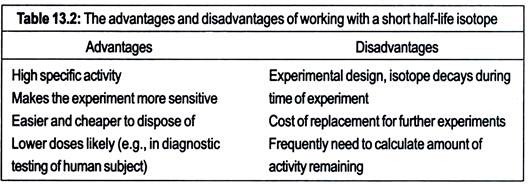
The values of t1/2 vary widely from 1019 years for lead-204 (204Pb) to 3 × 10-7s for poloruum- 212 (212Po). The half-lives of some isotopes frequently used in biological work are given in Table 13.1. Note that two important elements, oxygen and nitrogen are missing from the table. This is because the half-lives of radioactive isotopes of these elements are too short for most biological studies (15O has t1/2 of 2.03 min, whereas 13N has 11/2 of 10.00 min). The advantages and disadvantages of working with isotopes of differing half-lives are given in Table 13.2.
Units of Radioactivity:
The System International Unites (SI system) uses the Becquerel (Bq) as the unit of radioactivity. This is defined as one disintegration per second (1 d.p.s.). However, an older unit, not SI system and still frequently used is the curie (Ci). This is defined as the quantity of radioactive material in which the number of nuclear disintegrations per second is the same as that in 1 g of radium, namely 3.7 × 1010 (or 37 GBq).
For biological purposes this unit is too large, and the micro curie (µCi) and millicurie (mCi) are used. It is important to realize that the curie refers to the number of disintegration actually in a sample (i.e., d.p.s.) not to the disintegrations detected by the radiation counter, which will generally be only a proportion of the disintegrations occurring and are referred to as counts (i.e., c.p.s.).
Normally, in experiments with radioisotopes, a carrier of the stable isotope of the element is added. It, therefore, becomes necessary to express the amount of radioisotope present per unit mass. This is the specific activity. It may be expressed in a number of ways including disintegration rate (d.p.s. or d.p.m.), count rate (c.p.s. or c.p.m.) or curies (mCi or µCi) per unit of mass of mixture (units of mass are normally either moles or grams).
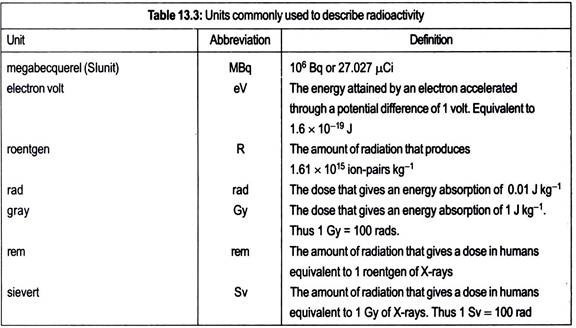
An alternative method of expressing specific activity, which is not very frequently used, is atom percentage excess. This is defined as the number of radioactive atoms per total of 100 atoms of the compound. For quick reference, a list of units and definitions frequently used in radiobiology is provided in Table 13.3.