Read this article to learn about the basic principles of radioactivity.
Radioactivity is a phenomenon that occurs naturally in a number of substances. Atoms of the substance spontaneously emit invisible but energetic radiations, which can penetrate materials that are opaque to visible light.
The effects of these radiations can be harmful to living cells but, when used in the right way, they have a wide range of beneficial applications, particularly in medicine.
Radioactivity has been present in natural materials on the earth since its formation (for example, in potassium-40 which forms part of all our bodies). However, because its radiations cannot be detected by any of the body’s five senses, the phenomenon was only discovered 100 years ago when radiation detectors were developed.
Nowadays we have also found ways of creating new man made sources of radioactivity; some (like iodine-131 and molybdenum-99) are incidental waste products of the nuclear power industry which nevertheless have important medical applications, whilst others (for example, fluorine-18) are specifically produced for the benefits of their medical use.
Other Principle Aspects of Counting Radioactivity and Analysis of Data:
Assessing the presence and amount of radioactivity is invariably accomplished by radiations emitted.
The difference between amount of radiations emitted and detected actually depends on number of factors which can be classified as follows:
1. Counter Characteristic:
(a) Background count:
Radiation counter of all types always register an “unwanted” background count, even in the absence of radioactive material in the apparatus. This may be due to such sources as cosmic radiation, natural radioactivity in the vicinity, nearby X-ray generators, and/or circuit noises and may interfere in a measurement.
By means of the various methods already outlined and the use the lead shielding, this background radiation may be considerably reduced, but its values must always be recorded and accounted for in all experiments. Some commercial experiments have automatic background sub traction facilities.
(b) Dead time:
Detector systems (like GM Counter) designed for quantitative measurement has electronic equipment to count and record the number of pulses received from detector. All such equipments require a finite time to record a pulse, and during this time it is “dead” to any other pulse which may arrive.
Thus at very high count rates in Geiger- Muller counting, counts are lost due to the dead time of the Geiger-Muller tube. (Correction tables are available and those should be used when necessary to correct for lost counts. Dead time is not a problem in scintillation counting.
(c) Geometry:
Those factors which determine whether the radiation misses or hits the detector are collectively referred to as counting geometry.
These factors are:
1. Geometric relationship between the source of the radiation and detector.
2. The presence of material which absorbs or scatters the emitted radiation. Therefore, when samples with an end- window ionization counter, such as a Geiger- Muller tube, are compared, it is important to standardize the position of the sample in relation to the tube, otherwise the fraction of the emitted radiation entering the tube may van’ and hence will vary the observed count.
2. Sample and Isotope Characteristic:
(a) Self-absorption:
Self-absorption is primarily a problem with low energy P emitters; radiation is absorbed by the sample itself. Self-absorption can be a serious problem in the counting of low energy radioactivity by scintillation counting if the sample is particulate or is, for instance, stuck to membrane filter. Care should be taken to ensure comparability of samples because the methods of standardization outlined earlier will not correct self- absorption effects.
When homogeneity is not possible, particulate samples should be digested or otherwise solubilized prior to counting. Self-absorption is a major problem with Geiger-Muller counting and significantly reduces sensitivity and reliability. It is very difficult to count low energy emitters reliably with these counters and this was a major factor in the switch to scintillation counting.
(b) Half-life:
The half-life of an isotope may be short and, if so, this must be allowed for analysis of the data.
(c) Statistics:
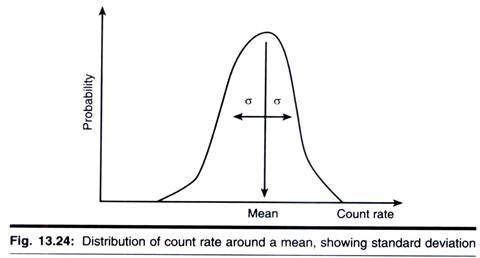
The emission of radioactivity is a random process. This can be demonstrated readily by making repeated measurements of the activity of long-lived isotope, each for an identical period of time. The resulting counts will not be the same but will vary over a range of values, with clustering near the centre of the range. If a sufficiently large number of such measurements is made and the data are plotted, a normal distribution curve will be obtained.
For a single, therefore, we cannot obtain a true count. Instead we take the mean of a large number of counts as being very close to the true count. However, the accuracy of this mean will depend on the spread or standard deviation (σ) for the data. Statistical theory states that, for a normal distribution 68.2% of values obtained lie ± 1σ, and 95.5% lie + 2σ from the mean (x).
Clearly, if we wish to compare samples, and in particular to state that two samples con am different amounts of radioactivity, then we need to take account of the counting statistics. Fortunately Poisson mathematics makes the task relatively easy as;
For example, if 1600 counts are recorded, this can be expressed as 1600 ± 80. There is, therefore, a 95.5% chance that the true figure lies between 1520 and 1680.
When data are expressed as d.p.m. or c.p.m, again using 95.5% certainty, then error on;
and therefore 160 c.p.m. ± 8 c.p.m. Note that the error is the same. This is because effectively the same number of measurements, i.e., counts, has been taken in each case.
If we had recorded 160 counts in only 1 min, then;
In summary, the counts per minute data become more accurate for higher count rates and/or longer counting times. It is a common practice to count 10000 counts or for 10 min, whichever is the quicker, although for very low count rates longer counting times are required.
3. Supply, Storage and Purity of Radiolabeled Compound:
There are several suppliers of radiolabelled compounds, the main ones being Amersham Biosciences plc. Du Pont, NBN and ICN. The suppliers usually include details of the best storage conditions and quality control data with their production. This is because several types of decompositions can occur; for example internal decomposition resulting from radioactive decay such as 14C → 14N, and external decomposition where emitted radiation is absorbed by other radioactive molecules, causing impurities.
The extent to which decomposition occurs is dependent on many factors such as temperature, energy of radiation, concentration and the formulation of the compound. It is therefore, imperative to store radioisotopes by the method recommended by the supplier and to maintain sterility of the stock. If necessary, chromatographic procedures will be required to check on the purity of the labelled compound.
4. Specific Activity:
The specific activity of a radioisotope defines its radioactivity related to the amount of material (e.g., Bq mol-1 Ci mmol-1 or d.p.m. µmol-1). Suppliers offer a range of specific activities for their compound, the highest often being the most expensive.
The advantages of using a very high specific activity are as follows:
i. Products of a reaction using the labelled precursor can be produced at high specific activity (e.g., for DNA probes).
ii. Small quantities of radiolabelled compound can be added such that the equilibrium of metabolic concentrations is not unduly pertubated.
iii. (Calculating the amount of substance required to make up radioactive solutions of known specific activity is simplified, as the contribution to concentration made by the stock radiolabelled solution is often negligible.
Sometimes, however, it is not necessary to purchase the highest specific activity available. For example, enzyme assays in vitro often require a relatively high substrate concentration and so specific activity may need to be lowered.
Consider the example below:
[3H]Leucine is purchased with a specific activity of 5.55 TBq mmol-1 (150 Ci mmol-1) and a concentration of 9.25 MBq 250 mm‑3 µCi 250 mm-3). A 10 cm3 solution of 250 mM and 3.7 kBq cm-3 (0.1µCi cm-3) is required.
It is made up as follows:
i. 10 cm3 at 3.7 kBq cm-3 is 37 kBq (1µCi), therefore, pipette 1 mm3 of stock radioisotope into a vessel (or, to be more accurate, pipette 100 mm3 of a × 100 dilution of stock in water).
ii. Add 2.5 cm3 of a 1 M stock solution of cold leucine, and make up to 10 cm3 with distilled water.
There is no need to take into account the amount of un-labelled leucine it the (3H] leucine preparation; it is a negligible quantity due to the high specific activity. If necessary (e.g., to manipulate solutions of relatively low specific activity), however, the following formula can be applied;
W = Ma [(1/A’) – (1/A)],
where, W is the mass of cold carrier required (mg), M is the amount of radioactivity present (M Ben a is the molecular weight of the compound, A is the original specific activity (M Bq mmol-1), and A’ is the required specific activity (M Bq mmol-1).
5. The Choice of Radionuclide:
This is the complex question depending on the precise requirements of the experiment. A summary of some of the key features of radioisotopes commonly used in biological work is shown in the table in above sections.