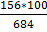The below mentioned article provides an overview on Probability:- 1. Introduction to Probability 2. Mathematical Probability and Statistical Probability 3. Rules or Theorems of Probability 4. Probability Distribution.
Contents
Introduction to Probability:
Probability means possibility or likelihood for the occurrence of a specific event, as for example, the likelihood of winning the cricket match. If several events are taking place, the possibility for the occurrence of any specific event can be predicted.
Thus, if a coin is tossed 100 times, it is likely that it will fall “head” 50 times and “tail” 50 times because chances for turning up of head and tail are equal, i.e., 1:1. When an experiment results in two or more different results, the experiment is called trial and the results obtained from the experiment are called events.
The likelihood of any specific event may be influenced by several factors. For example, the result of an examinee depends on his performance, the type of question paper (easy or hard), evaluation of answer books by the examiners etc.
Contrary to such events, there are some events whose occurrence is not affected by any factor other than chance, as for example, when a coin is tossed, either head or tail turns up and similarly, the sex of a new born baby is either male or female.
When several events occur at a time, then the probability of occurrence of a specific event will be equal to number of times that event happens divided by the total number of opportunities for it to happen or total number of trials.
P = 1/n
Where P = Probability of any event, and
n = total number of trials.
Value of p does not exceed 1 and all the values of P lie between O and 1.
In the same way, the probability of failure of any specific event may be calculated as follows:
P = No. of cases not favourable/Total number of trials
If the total number of trials is represented by n and the number of times any specific event (A) happens is m, then
P (A) = m/n
If m represents the number of favourable cases out of total number of events (n) the number of failures or non-favourable cases (A̅) will be n-m, and then the probability of the failure of event P(A̅) will be
If a cubical die having six sides or faces mentioned 1,2,3,4,5 and 6 is rolled, any one of the 6 different faces may turn up. Here, the group of six possible results is said to be exhaustive and the rolling of die is called a trial. Here the probability of rolling a “four” on a die in a single trial or p (4) will be 1/6, because, the die has six faces. As each face is likely to turn up, the average result should be one four for every six trials.
Example:
Final out the probability of birth of male child to an expecting women.
Solution:
There are two conditions in this case, i.e., the new born may be either a male child or a female child. So n = 2, and each condition stands one chance out of two. Therefore, the probability for a boy would be
P(B) = 1/n =1/2
and similarly, probability for a girl P(G) = 1/n = 1/2
Types of Events:
The events are of several types, some of which are defined here as under:
1. Simple Events:
When a single event occurs at a time, this is called simple event, as for example, taking out a single card from the stack of playing cards.
2. Compound Events:
When two or more events occur simultaneously. They are called compound events, as for example, turning up of heads when two coins are tossed simultaneously.
3. Mutually Exclusive Events:
When two events are so related that the occurrence of one prevents the occurrence of the other or vice-versa in a trial, they are said to be mutually exclusive events. For example, tossing of a coin is a trial which provides an equal opportunity for the head or tail to turn up and in the trial only one, either head or tail can occur but not both.
Similarly, a new born baby can be a boy or a girl. Thus, the occurrence of boy excludes that of girl and vice-versa. Therefore, these events are mutually exclusive events.
The probability of mutually exclusive events is determined by the following simple formula:
P = 1/n
When two mutually exclusive events are such that the possibility of occurrence of one event is neither less nor more than the possibility for the occurrence of other event, they are said to be equally likely events. For example, when a coin is tossed, the possibilities for turning up of head or tail are equal and thus, the two are equally likely events.
4. Independent Events:
When two or more events are so related that the occurrence of one does not affect the possibility of the occurrence of remaining event(s), they are said to be independent events. For example, when two coins A and B are tossed together or separately, the head or tail of coin A does not affect the possibility of the occurrence of head or tail of coin B. Thus, turning up of head or tail of coin A is independent of that of coin B.
If coin A and B are tossed together, one may obtain any of the following combinations of events:
(i) Head of both coins,
(ii) Head of coin A and tail of B,
(iii) Tail of coin A and head of B, and
(iv) Tail of both A and B.
Table 32.1 Probability of different combinations of head and tail of coin A and coin B tossed either simultaneously or separately.
The combination of head of coin A and tail of coin B and tail of coin A and head of coin B may be grouped together since both of them have head and tail and the only difference between the two is the particular coin in which head or tail appears first.
The condition of getting one head and one tail on tossing the two coins is satisfied by both these conditions. Therefore, the possibility of getting one head and one tail will be the sum of the probabilities of these two combinations (1/4 + 1/4 = 1/2).
This is so because such combinations of independent events behave as mutually exclusive events.
Similarly, when three coins are tossed simultaneously, the following eight combinations of head and tail are possible: HHH, HHT HTH, THH, HTT, THT, TTH and TTT Each of these combinations will have the probability of 1/8 = (1/2 × 1/2 × 1/2).
These eight combinations ignoring the sequence of occurrence of head (H) and tail (T) can be grouped in the following four classes:
(i) One combination of three heads (HHH).
(ii) Three different combinations of 2 head and one tail- (HHT, HTH, THH).
(iii) Three different combinations of one head and two tails- (HTT, THT, TTH).
(iv) One combination of three tail-TTT.
Thus, the possibilities of getting 3 heads, 2 head and one tail, one head and two tail and three tail on tossing three coins simultaneously will be 1/8, 3/8, 3/8, and 1/8 respectively. The number of possible combinations of head and tail on tossing 4, 5,6, and 7 coins together will be 16,32,64 and 128 respectively.
This indicates that the number of different combinations increases with the increase of the number of independent events. Increase in the number of independent events by one will double the number of possible combinations.
5. Dependent Events:
When the occurrence of one event affects the occurrence of other and vice- versa such related events are said to be dependent events.
6. Sample Space or Probability Space:
All the possible results of an experiment or trial form a set which is referred to as sample space or probability space. For example, a woman gives birth to a child that may be a male or female. Therefore, the sample space = M, F. If two women give birth to one baby each, the probability space (S) may be MM, MP, FM, FF.
7. Conditional Events:
When two events are so related that one occurs either before or after the other, they are said to be conditional events.
Suppose, for example, there are two events E1, and E2 which may be defined as follows:
(i) E1/E2 which means that E1 occurs after E2.
(ii) E1/E2 which means that f2 occurs after E1.
Mathematical Probability and Statistical Probability:
When the probability is calculated on the basis of reasoning even before any trial or experiment hat is called mathematical or apriori probability. In practice, the actual probability calculated by trials may not coincide with apriori probability, for example, when a coin is tossed one gets the head (H), though the mathematical probability of occurrence of head is only 1/2 in the trial P (H) = 1 or P(H) = O.
But if the coin is tossed 10 times, the occurrence of head (H) can be O or 1 or 2 or 3 – or 10, the extreme cases being very rare. Suppose H occurred 4 times out of 10 trials. Now consider the occurrence of H as the favourable event, the occurrence of H 4 times out of 10 trials gives the relative frequency 4/10 for H (The apriori probability is 1/2).
But if the number of tosses (trials) is increased, it is likely that the ratio of the occurrence of favourable event becomes more close to 1/2. In general, if favourable event, say head (H), occurs n time out of N trials, the relative frequency of favourable event will be n/N. The limit of this relative frequency as N becomes infinitely large is known as statistical probability.
Rules or Theorems of Probability:
The concept of probability is of paramount importance in statistics as it provides the basis for all the tests of significance.
It is usually estimated on the basis of the following two basic rules of chances:
1. Addition rules or addition theorem.
2. Multiplicative rule or multiplication theorem.
1. Addition Rule of Probability:
This rule is applied when two events are mutually exclusive, i. e., both events do not occur simultaneously. Suppose that E1 and E2 are mutually exclusive events and the occurrence of one event precludes the occurrence of the other event. The probability of occurrence of either E1and E2 is the sum of the probabilities of the individual events. P(E1)or P(E2) = P(E1) + P(E2) .
This addition rule of probability can be extended to any number of mutually exclusive events as follows:
P (E1 or E2 or E3 …. or En) = P (E1) + P (E2) + P (E3) + ……. P (En)
If a coin tossed, the probability of the occurrence of one face of that of other face is equal to the probability of one face plus the probability of the other face, i.e.,
P (H) or (T) = P (H) + P (T) = 1/2 + 1/2 = 1.
Problem:
In a bunch of 8 flowers, four are red and the others are white. Find out the probability that (i) one flower drawn from the bunch at random is red, (ii) two flowers drawn from the bunch at random are of the same colour.
Solution:
(i) As all the 8 flowers of the bunch have equal chance for being drawn and there are 4 red flowers out of 8, the probability of selection of a red flower in a random chance is 4/8 = 1/2
(ii) The two flowers selected at random can be both red or both white. So the required probability = Probability of selecting two red flowers + probability of selecting two white flowers because both are mutually exclusive and equally likely events.
The number of ways in which two flowers of the same colour (red or white) can be selected from 4 flowers of one colour is six because if red flowers are numbered R1, R2, R3, R4 and white flowers are numbered W1 W2, W3 W4, the possible combinations areR1R2,R1R3, R1 R4, R2R3,R3, R4and R3 R4 of red flowers and W1 W2, W1 W3, W1 W4, W2 W3, W2 W4, W3 W4 of white flowers.
In general, the number of combinations of two from n different things (“C2) is calculated by the formula:
The number of combination of 3 from n different things is determined by the formula:
So the probability of getting at random two flowers of red colour from 4 is ![]()
And the number of combinations of 2 from 8 different things is ![]()
Therefore, the probity of drawing two flowers of red colour is 6/28 and the probability of two flowers is 6/28 + 6/28 = 12/28 = 3/7.
(iii) Multiplicative Rule of Probability:
This theorem states that the probability of two independent events occurring simultaneously is the product of individual probabilities of those events.
If P (E1,) and P (E2) are the probabilities of independent events E1 and E2, then the probability of the two events happening together is calculated as follows:
P (E1) + P (E2) = P (E1) x P(E2)
This theorem can be extended to any number of independent events as follows:
P (E1, E2, E3 …..En) = P (E1) x P (E2) x P (E3) x …….x P (En).
Problem:
In a flock of 16 birds, the ratio of black feathered birds to white birds was 5:3.
If three birds are drawn at a time at random, find out the probability that:
(i) They are all black,
(ii) They are all white, and
(Hi) They all are either black or white.
Solution:
Since the ratio of black birds to white birds is 5:3, out of 8 birds, the ratio of black to white out of 16 birds will be 10 black and 6 white.
(ii) The number of ways in which three white birds are selected in a draw out of 6 white birds is:
So, the probability of getting 3 white birds in a draw at random from a flock of 16 birds is:
(iii) In a draw of three birds at a time, the probability of getting all three birds of either black colour or of white colour will be the same as of individual probability of black birds and white birds:
Probability Distribution:
The characters which show variation are referred to as random variables or variates. They may be discrete or continuous.
On the basis of nature and probability of occurrence of random variables, the following three types of probability distribution have been formulated:
1. Normal probability distribution.
2. Binomial probability distribution.
3. Poisson probability distribution.
1. Normal Probability Distribution:
The normal form of distribution was worked out by De Moivre (1733) which was further developed by Gauss (1809) and Leplace (1812). For this reason normal probability distribution is named after these workers. Gauss noted that the errors of observations on any character follow normal distribution. Therefore, the normal probability distribution is also referred to as Gaussian law of error.
The term normal does not stand for normal trend of any character nor it stands for the norm of distribution of any character. In fact, normal distribution is the distribution of characters showing continuous variation.
In binomial distribution (p+q)n, if the value of power n is infinite and all the frequency points are linked by a line on graph paper, a simple curved line will be obtained. That is called normal frequency distribution curve (Fig.32.1). The shape of normal distribution is unimodel, symmetrical and the ends of the curve tail off to the base. Graphically total area under the curve is unity.
The algebraic equation of normal distribution curve is ![]() where µ = population mean and σ = standard deviation when frequency of a character is N and distribution is normal then the frequency
where µ = population mean and σ = standard deviation when frequency of a character is N and distribution is normal then the frequency ![]()
2. Binomial Distribution of Probability:
Binomial probability distribution has been worked out by James Bernoulli. The law of probability of coincidence of independent events states that the chance or probability of the simultaneously occurring two or more independent events is the product of the individual probabilities of the events.
If two independent events E1 and E2 occur simultaneously and their probabilities are p and q. respectively, then the probability of their joint occurrence will p × q.
For example, suppose if 10 coins are tossed together one may get 5 heads and 5 tails, 4 heads and 6 tails, 3 heads and 7 tails most frequently, other results less after and either 10 heads and no tails or vice-versa rarely. When the number of respective heads and tails of different tosses of coins are plotted on graph paper, a symmetrical graph (curve) would be obtained.
This is called symmetrical or normal probability curve. Here if P stands for probability of head, q stands for probability of the tail and n stands for the number of coins, the probability of head (p) and the probability of tail (q) are both equal to 1/2 In other words, for one coin, the distribution of probability will be or (p + q)2.
If two coins are tossed together, the following probability can be expected:
So the probability distribution = p2 + 2pq + q2 = (p + q)2
This is an expansion of general binomial (p + q)n.
For different values on n, the following expansion of (p+q)n can obtained:
The complete expansion of the binomial (p + q)n involves two steps. The first step involves the determination of various terms of expansion and the second step involves the determination of co-efficient of these terms. The first term obtained on simplification of binomial (p + q)n is pn qn or pn(as qo =1).
In the subsequent terms, the index of p sequentially decreases by 1 and that of q sequentially increases by 1 till it reaches poqn or qn. Simplification of (p + q)n in this way yields the following expansion:
In the above expansion each term has an appropriate co-efficient. The co-efficient of the term can be calculated by the following general formula:
When n = index of binomial, S = index of p in the term and t = index of q in the term and ! = factorial, e.g., n! = 1 × 2 × 3 × …………………n, S! = 1 × 2 × 3…………………×S, t! = 1 × 2 × 3 ×……….×t (in other words, 3! = 1 × 2 × 3, 4! = 1 × 2 × 3 × 4, 5! = 1 × 2 × 3 × 4 × 5 and so on.
The set of terms written along with their appropriate co-efficients constitutes the complete binomial expansion.
Calculation of Probabilities using Binomial Expansion:
The binomial expansion can be used only in the case of two mutually exclusive events. The binomial expansion appropriate for a problem has the same index as are the number of independent events in the problem. One of the two mutually exclusive events is represented by p and the other is represented by q. Indices of p and q in a term is the same as the numbers of mutually exclusive events they represent.
The probability of a given combination of mutually exclusive events is obtained by simplifying the term of binomial expansion which is appropriate for that combination.
The steps for calculation of probability of occurrence of a combination of two exclusive events are as follows:
(a) Selection of binomial appropriate for the problem. The binomial appropriate has the same index as are the independent events in the problem.
(b) Expansion of binomial along with the co-efficient of the various terms of binomial.
(c) Selection of appropriate term. In the term appropriate to a combination of independent events, the index of p is equal to the number of one exclusive event in combination while that of q is equal to the number of other mutually exclusive event.
(d) Simplification of selected term. For simplification p and q are replaced by the probabilities of the events they represent.