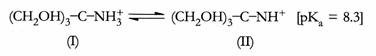Buffers: pH, Capacity and Ionic Strength!
pH: The negative logarithm of the hydrogen ion concentration, the pH, is expressed as follows:
pH = -log10[H+]
The pH scale is a measure of hydrogen ion concentration that eliminates dealing with large powers of 10 and compresses a large range of concentrations onto a more convenient scale, between 1 and 14. At a high concentration of H‑ (10-1M), the pH value is low, pH = 1. While at low concentration (10-12 M), the pH is high, pH = 12.
Hydrogen ions in the solution arise from the dissociation of acids.
HA → H+ + A
Strong acids are considered to be completely dissociated into ions in dilute solution. However, weak acids (or bases) are only partially dissociated in solution, and thus equilibrium is established between ions and the un-dissociated molecules.
HA ↔ H+ + A–
The equilibrium constant Ka, is defined as follows:
Ka = [H+] [A–] / [HA]
Where HA = un-dissociated acid, H+ = hydronium ion, and A– = conjugate base. From this expression we can derive Henderson-Hasselbach equation, commonly called buffer equation, which relates pH of solution to the pKa of the acid and the relative concentration of un-dissociated acid and the conjugate base forms. The Henderson-Hasselbach equation is
pH = pKa + log [Conjugate base] / [acid].
It is most useful in the preparation of buffers and in understanding how the concentration of the acid and conjugate base forms of a weak acid affect the pH.
Buffers:
A buffer, by definition, resists changes in the pH of the solution. A buffer must contain the chemical species for “neutralizing” added amounts of acid or base. Generally, a buffer is a solution of a weak acid and its conjugate base (e.g., ammonia and ammonium chloride). A buffer is selected on the basis of its pKa and its chemical nature. As shown by Henderson-Hasselbach equation, when concentrations of the conjugate base and the un-dissociated acid are equal, the pH of the solution equals pKa of the buffer
pH = pKa + log 1
log 1 = 0,
pH = pKa.
When [conjugate base] = 10 × [acid], then
log [conjugate base]/[acid] = log 10 = 1,
pH = pKa + 1
When [conjugate base] = 1/10 [acid], then
log [conjugate base]/[acid] = log 1/10 = – 1
and
pH = pKa – 1.
Thus, buffers are most effective in the range pH= pKa ± 1. Outside that range, the concentration of either the acid or the conjugate base is too small to effectively resist the effects of added hydrogen or hydroxide ion.
Once the desired pH range for an experiment has been decided, one can select a buffer on the basis of pKa value. Since temperature affects the dissociation of some weak acids and bases and thus the pKa value, buffer should always be pH adjusted for the temperature at which they will be used. Following table shows the effect of temperature on some important buffers.
For example, widely used buffer Tris [trid (hydroxymethy) amino methane] shows a change in pKa of – 0.031 for each degree change in temperature from reference temperature of 20oC(∆pKa/ °C). Therefore, at 10°C the change in pKa = (10°C – 20°C) (-0.031) = 0.31; the pKa at 10°C is 8.3 + 0.31 = 8.6.
Buffer Capacity and Ionic Strength:
The molar strength of the two components of the buffer should be chosen to give adequate buffering capacity. The total ionic strength of the buffer may also be an important consideration; for example, in enzyme studies. The buffer strength is expressed in terms of the total concentration of conjugate base or conjugate acid. Again, let us use Tris as an example.
The pKa for tris is 8.3 at 20°C; therefore, this substance can effectively serve as a buffer between pH 7.3 and 9.3. To make a 50 mM Tris buffer with pH = 7.8, start with either the free base (II) or the hydrochloride salt, Tris-HCol. A 50 mM solution contains 50 mmol of solute per litre of solution. Tris, the free base form, has a molecular weight of 121.1 g. the amount of solid Tris needed to make one litre of 50 mM solution is
50 mmol × 121.1 mg/mol = 6055 mg Tris.
However, pH of the solution is needed to be adjusted to 7.8 with acid. Hydrochloric acid would be the best choice because Tris-HCl is soluble and chloride ion is best compatible with most of the biological systems. The chemical nature of the buffer is especially important in biological investigations — solubility, stability, defined interaction with other ions in the system, light absorption, and potential inhibition or stimulation of the function are all criteria to consider in buffer selection. The zwitterionic buffers do not pass through the biological membrane and do not complex cation such as Ca2+ and Mg24. All these buffer has tertiary amine function that dissociates in pH range 6-9.