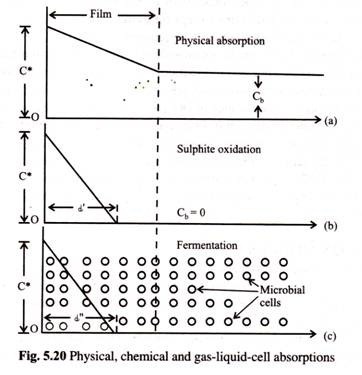
Competition for resources that occurs between members of different species is called inter-specific competition.
Competition for food also applies to individuals of different species that require the same type of food.
For example, two different predatory species may compete for the same prey species.
The severity of inter-specific competition depends on the extent of similarity or overlap in the requirements of different individuals and the shortage of supply in the habitat. Such a competition may have the following effects on the population.
The eight effects of inter-specific competition on population are as follows:
1. Regulation of Population Size 2. Segregation of Species into Different Niches 3. Competitive Exclusion Principle 4. Exploitative Competition 5. Interference Competition 6. Competition and Biological Variation 7. Competition and Character Displacement 8. Logistic Equation and Interspecific Competition.
1. Regulation of Population Size:
The role of competition in regulating population size is directly effective by causing mortalities through fighting, nest destruction and loss of food supplies. In also results into increased predation and dispersal into other regions.
2. Segregation of Species into Different Niches:
Inter-specific competition is the most critical factor that confines a species to a particular niche. This becomes evident with the expansion of the species beyond the usual limits of its niche when this competition is over. Thus, inter-specific competition results in the segregation of species into different niches.
3. Competitive Exclusion Principle:
The principle has been variously named after its principal authors – Gause’s principle (Lack, 1944), Volterra – Gause principle (Hutchinson, 1957) and Hardin’s competitive exclusion principle. Gause’s competitive exclusion principle states that no two species can coexist if they occupy the same niche. In other words, an ecological niche cannot be simultaneously and completely occupied by stabilized populations of more than one species.
In his classic experiment Gause (1934) first grew Paramecium caudatum and Paramecium Ha in separate cultures and found that each species grew in numbers according to the logistic equation. However, P. aurelia grows in numbers more quickly than P. caudatum and shows more individuals in the same volume of culture medium.
But when he grew the two species together in same culture volume, he observed that initially both species grew in numbers, but eventually P. caudatum declined and became extinct (Fig. 3.6 ). He repeated has experiment and found that P. aurelia always won the competition between the two species. Gause attributed the result to the nee of ‘but a single niche in the conditions of the experiment’.
There are other examples illustrating the principle of Gause. Park( 1948,1954,1962) conducted laboratory experiments on two species of flour beetle, Tribolium confusum and Tribolium castaneum. He found that in mixed cultures one species always “wins” over another. But it depended on the environmental conditions. T .castaneum always wins (or T. confusum becomes extinct) under conditions of high temperature (34°C) and high humidity (70% R.H), while T. confusum always (T. castaneum becomes extinct) under cool-dry climate, i.e., under conditions of low temperature and low humidity (30% R.H.). Under some different environmental conditions (Table 3.1) time’s one species survived, sometimes the other. This leads us to conclude that species can coexist even in the face of interspecific competition provided that their niches do not overlap too much.
4. Exploitative Competition:
Competitive interaction may cause exploitation, which develops when two species are competing die same resource. When two flour beetles, T. confusum and T. castaneum, are kept together, one of them drives out the other in competition depending upon the laboratory conditions. However, when their cultures were infested with Adelina, a sporozoan parasite that may kill the beetles, it was found to have important effect on T. castaneum but no on T. confusum.
These experiments have demonstrated that the outcome of competition is no invariable but rather is affected both by extrinsic factors like weather and parasites and by intrinsic properties like the genetic composition of the competing populations.
5. Interference Competition:
It may be defined as competition in which individuals actively interfere with one another’s access to resources. It occurs when two species are not competing in the exploitation sense, but when their coexistence in the same habitat modifies some behavioural pattern of one or the other For example, the smell or mere sight of a male mouse of a different species may cause abortion in recently fertilized females of some species. When both exploitation and interference develop between sympatric species, the competition is most intense.
6. Competition and Biological Variation:
The selective effects of competition naturally affect the extent of variation that is maintained in species populations. The effect will be related to the taxonomic nature of the competing populations. If the habitat is occupied by a species population composed of interbreeding but geographically or ecologically discrete segments, such as subspecies or ecotypes, competition between them will tend to extend variation within the individual populations until it approximate to the variation within the habitat.
In other words, the overall tolerance range of the species will widen or competition will tend to widen the biological variation already present in the segments if, on the other hand, the habitat is occupied by competing independent species populations, gene flow will accordingly be very much restricted.
The pressure of inter-specific competition will in this case select from each species population those genomes that confer a special adaptation to particular and limited range of the environment. In this case the competition will, therefore, tend to narrow the biological variation present in each of the competing species.
7. Competition and Character Displacement:
Character displacement is defined as the divergence in the characteristics of two otherwise similar species where their ranges overlap, caused by the selective effects of competition between the species in the area of overlap.
In the phenomenon of character displacement, the character traits of two closely related species differ more when they occur in sympatry (two species coexisting within the same geographic area) than in allopatry (when their distributions do not overlap, they are said to be allopatric). The ground finches (Geospiza spp.) of Galapagos Islands, first described by Darwin, furnish an example of character displacement. Character displacement occurs when inter-specific competition results in natural selection causing changes in the morphology of two closely related species.
8. Logistic Equation and Interspecific Competition:
For a single population, i, we may write the logistic equation –
dNi/dt = ri Ni (1 – Ni/Ki)
In this equation all the parameters have been subscripted to show that they are specific to population i. Intra-specific competition appears as the term Ni/Ki. As Ni approaches Ki, Ni/Ki approaches 1 and the quantity (1 – Ni/Ki) approaches 0. A stable equilibrium (dNi/dt = 0) is reached when Ni = Ki.
If there is a population j that competes with population i for resources; and population J has a density Nj and a carrying capacity Kj. Naturally the competitive pressure of population j will have a negative effect on population i and will reduce the growth rate of population i. This idea may be incorporated into the logistic equation by subtracting a term that represents the effect of interspecific competition (with species j on species i).
dNi/dt = ri Ni (1 – Ni/Ki – [Competitive effect of j on i] )
This equation now includes terms for both intra-specific competition (Ni/Ki) and inter-specific competition. Both terms act as discounting terms (subtractions) and the equation may be written as: dNi/dt = ri Ni (1 – [intra-specific competition] – [competitive effect of j on i] It must be appreciated that in this model the intra-specific and inter-specific effects are independent of each other. In order to show an interaction between the two effects, we must include a term where the product of the two was subtracted from 1.
Volterra incorporated inter-specific competition into the logistic equation by incorporating the term aij Nj/Ki into the quantity within the parantheses. Hence equation becomes –
DNi/dt = ri Ni (1 – Ni/Ki – aijNj/Ki)
Where Nj = the number of individuals of the competing species j
aij = coefficient of competition
The coefficient of competition may be defined as a measure of the degree to which one species, j, utilizes the resources of another, i, expressed in terms of the population consequences of the interaction. In other words, aij is the effect of an individual of species j on the exponential growth rate of the population of species i. The multiplication of aij by Nj (the size of the competing population j) converts the population of the competing species into units of species i on which it has an effect.
Dividing the product aij Nj by Ki, as shown in the equation, gives the proportion of the carrying capacity of i that is taken up by equivalent units of individuals of i. However, population i will also have some competitive effect on population j.
This may be shown by the following equation:
dNj/dt = rjNj (1 – Nj/Kj – ajiNi/Kj) This equation shows how intraspecific competition in population j and the competitive effect of population i on population j, affect the growth rate of population.