The following points highlight the four major steps involved in the construction of taxonomic groups. The steps are: 1. Operational Taxonomic Units 2. Unit Characters 3. Estimation of Resemblances 4. Cluster Analysis.
Contents
Taxonomic Group: Step # 1.
Operational Taxonomic Units (OTUs):
Operational taxonomic unit is the basic unit in numerical taxonomy. It can be an individual, species, genus, family, order or class. Since the taxonomic units employed in numerical methods are not always comparable to formal taxonomic units, they are termed as operational taxonomic units. Comparison of OTUs of equal rank is always made in numerical taxonomy.
In case of OTUs above the level of individual, adequate representation of various polymorphic forms is essential. For example, when genera are compared, they should be represented by different species. Similarly, when families are compared, they should be represented by different genera and so on.
Taxonomic Group: Step # 2.
Unit Characters:
Unit characters are the characters used in numerical taxonomy. According to Sokal and Sneath (1963), unit character is defined as a taxonomic character of two or more states, which within the study at hand cannot be subdivided logically, except subdivision brought about by changes in the method of coding. Only the phenotypic characters are used as unit characters, e.g. presence or absence of an awn in a grass spikelet.
(i) Types of unit characters:
Unit characters are of two types:
i. Binary characters:
Those unit characters, which exist in two states are called binary characters, e.g. presence or absence of trichomes. They can be represented by the simplest form of coding, where characters are divided into + and – or as 1 and. 0.
In such cases, the positive characters are recorded as + or 1 and negative characters are recorded as – or 0. In case the organ possessing a given character is missing in an organism, the character is scored NC, which means “no comparison“.
ii. Multistate characters:
Those unit characters, which exist in more than two states are called multistate characters. Such characters can be coded into number of states (1,2,3…) corresponding to their range of variation. They may be further of two types:
Qualitative multistate characters:
These characters contain three or more contrasting forms and each form is ranked on equal footing, e.g., flower colour, which can be in any number of states – red, white, purple, yellow, etc.
Quantitative multistate characters:
These characters represent measures of the size on a continuous scale, e.g., length of the leaf, which can be 2cm, 3cm, 4cm, etc., or height of the plant, or amount of pubescence on a leaf, etc.
(ii) Admissible unit characters:
The following characters can be categorized as admissible unit characters:
a. It cannot be subdivided.
b. It must show variation among the taxa under comparison.
c. It should be inherent in the organism.
d. It should not be susceptible to environmental changes or affected by experimented conditions.
e. It must be of some diagnostic value.
(iii) Inadmissible unit characters:
As in other disciplines of taxonomy, the proper selection of unit characters is a critical point in the application of numerical taxonomy. Sokal and Sneath (1963) have listed certain characters, which cannot be utilized for numerical taxonomy and called them as inadmissible characters.
These include:
a. Attributes, which are not a reflection of the genotypes of the organisms themselves.
b. Any property, which is a logical consequence of another, either partly or wholly.
c. Characters, which do not vary within the entire sample of organisms.
(iv) Proper selection of unit characters:
Sneath and Sokal (1973) have given the following suggestions for proper selection of unit characters:
a. They should come from all parts of the organism.
b. They should belong to all the stages of the life cycle of the organism.
c. Variable characters within the group should be used.
d. Due attention should be given to characters related to morphology, physiology, ecology and distribution of the organisms.
Taxonomic Group: Step # 3.
Estimation of Resemblances:
Most phenetic methods involve taxon-to-taxon distance, similarity or dissimilarity measures. Distance and dissimilarity are sometimes treated as the same thing, though a distinction can be made between them. As the name implies, distance and dissimilarity measure increase with dissimilarity between taxa, while similarity measures decrease with dissimilarity.
Thus the resemblance between two OTUs is estimated or measured either:
a. In terms of similarity i.e., percentage of characters in which they agree, or
b. In terms of dissimilarity i.e., percentage of characters in which they do not agree.
So far three methods have been devised for estimating the resemblance between the taxonomic groups, which include:
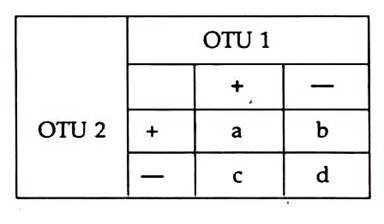
(i) Coefficients of association It is measured by the following formula:
S = Ns/ Ns + Nd
where, S is the numerical index or Simple matching index or coefficient;
Ns = the number of positive features shared by any two OTUs;
Nd = the number of positive features in one OTU and number of negative features in the other OTU.
Binary characters can be dealt with in two ways depending on whether they can be obviously polarized:
a. In terms of presence or absence, or
b. Whether the character simply has two states and it is undesirable or impossible to classify in terms of presence or absence.
Data are presented in the form of a truth table of test results between the two taxa or OTUs. Thus:
Simple matching index (S) or coefficient is defined as the number of tests giving identical results (a or d) divided by the total number of tests, thus
S= a + d / a + b + c + d (range 0 to 1)
(ii) Coefficients of correlation (r):
It is measured by the following formula:
where, j and k stand for two units under comparison;
Xij stands for the value of the character i in unit j;
Xik stands for the value of the character i in unit k;
Xi and Xk stand for the mean of all the characters in units j and k;
n stands for number of characters.
(iii) Measurement of taxonomic distance between OTUs:
Using the convention of multidimensional space with one dimension for each character.
Taxonomic distance (d) can be measured by the following formula:
where Xij is the character state of unit j for the character i;
Xjk is the character state of unit k;
n
Σ stands for the sum over n characters;
The value of the taxonomic distance (d) is the distance in a phenetic space divided by √n.
Taxonomic Group: Step # 4.
Cluster Analysis:
Cluster analysis or clustering is a type of multivariate statistical analysis. It is used to group organisms into separate clusters based on their statistical behaviour. The main objective of clustering is to find similarities between organisms, and then group similar organisms together to assist in understanding relationships that might exist among them.
Thus, different OTUs are grouped together on the basis of degree of similarity and these groups of OTUs are called clusters.
(i) Cluster analysis characteristics:
Cluster analysis is based on a mathematical formulation of a measure of similarity.
There are a number of characteristics that can distinguish different approaches to cluster analysis, which include:
a. Numerical, statistical, and conceptual clusters.
b. Agglomerative vs. divisive – Agglomerative methods start with individual taxa and seek to connect them into pairs, etc. in such a way that similarities between pairs or group members are maximized at each level. In contrast, divisive clustering splits are sought in the group of taxa that will in some way maximize the collective phenotype disparity between the two groups formed by the split.
c. Overlapping vs. disjoint clusters.
d. Incremental vs. non-incremental.
e. Flat vs. hierarchical representatives.
(ii) Clustering methods:
Clustering can be achieved in two ways:
a. Monothetic system — This system employs the attributes one at a time. The monothetic method obviously leads to artificial clustering.
b. Considering all their attributes simultaneously. This method gives a natural grouping.
One cluster or a group is separated from the other by a dividing line, which indicates a distinct gap between the two. In case of intraspecific clusters, there are often few discontinuities.
c. Phenetic clustering methods — Phenetic clustering methods have largely been overtaken by cladistic methods in order to relate data to evolutionary history, and they are now rarely employed in taxonomy as they often lead to substantially different clusters when applied to real data.
The most widely used phenetic clustering methods in taxonomy include the following:
i. Nearest neighbour clustering method — It is also called single linkage clustering. In this method, phenograms are constructed by joining OTUs and groups on the basis of their most similar members, i.e., the shortest distance. Whether an OTU will join an existing cluster depends on its maximum similarity (or minimum distance from) any member of that cluster.
The phenogram is initiated by joining the two (or more) most similar OTUs.
Sequence of procedures involved in the phenetic clustering of the above three taxa:
Furthest neighbour clustering method (complete linkage):
Construction of furthest neighbour phenogram is essentially similar to that for nearest neighbour ones, with the only difference that the OTUs are joined at a level corresponding to the greatest distance between their component members instead of the shortest distance as in case of the latter. This method tends to emphasize differences between clusters.
Unweight pair-group method using arithmetic averages (UPGMA):
In this method an OTU is joined to existing clusters on the basis of their average (mean) distance to the members of that cluster (Fig. 9.1). The mean distance between two clusters of OTUs is calculated by adding together the distances between all possible pair-wise combinations of OTUs in the two clusters and dividing by the number of combinations.
The tree construction method is similar to nearest neighbour clustering. Since this method uses mean distances, it is not so subjected to the effects of aberrant OTUs, and hence preferred over nearest neighbour methods.
Weighted pair-group method using arithmetic averages (WPGMA):
This is a set of methods rather than a single one. They are essentially similar to UPGMA except that, they weight distances such that there is a tendency to emphasize separations between large clusters.
They are also therefore less subjected to the effects of single or small groups of outliers and hence preferred over nearest neighbour methods. In this method, the distances are usually weighted by some function of the number of OTUs in each cluster.
Centroid clustering:
Its basic aim is similar to UPGMA and WPGMA, but it requires the actual taxa versus character raw data, or more precisely normalized data, rather than inter-taxon distances. This method makes use of the Euclidian distances within the character hyperspace between the centroids of clusters of OTUs (Fig. 9.2 & 9.3).
Euclidian distance is equivalent to the real physical distance by which the taxa would be separated if they were plotted in a space in which each axis represents one normalized variable and each axis is perpendicular to all others.
Calculation of Euclidian distance is shown below:
Differential shading of the similarity matrix:
This is a method to describe structure in matrices of similarity coefficients, in which similarity coefficients are grouped into five to ten evenly spaced classes, each of which are represented by different degrees of shading in the squares of half matrix.
Generally a darker shade is used for the highest value, and the lightest shade for the lowest value. Thus, the half matrix can be seen as a pattern to different shades, limited by a diagonal of squares with the darkest shade (Fig. 9.4a). Clusters can be more sharply defined by rearrangement of the sequence of OTUs (Fig. 9.4b).
Cluster analysis:
A large number of numerical techniques can be used to analyze the groups of related OTUs based on high similarity coefficients. These techniques include elementary cluster analysis, clustering by single, complete or average linkage, central or nodal clustering, etc. The groups of similar organisms organized in this manner are termed phenons, which are arbitrary and relative groups.
The clusters of phenons are then rearranged in a dendogram (Fig. 9.5), in which the mutually most similar taxa are paired and the pairs successively joined by the average similarity.
This finally results in a tree like dendogram when all units have been joined together, with the taxa at the tips of branches. The number of clusters is determined by drawing a horizontal (phenon line) intersecting the vertical lines of the dendogram.
The delimitation of phenons is done by drawing a horizontal line across the dendrogram at a similarity value. For example a line at 75%, creates five 75- phenons 1; 7; 3, 5, 6; 4, 9, 10; and 2, 8., If the OTUs 1 to 10 in the above dendrogram had been species, an 80-phenon line could indicate 6 subgenera and a 65-phenon line two genera.